静态程序分析学习笔记

介绍

南京大学《软件分析》课程：https://www.bilibili.com/video/av91858985/?spm_id_from=333.788.video.desc.click

当今编程语言的分类：

• 命令式：例如C、JAVA，程序可以按一条条命令拆解下来
• 函数式：例如PASCAL、Python（命令式和函数式相结合），将逻辑包含起来，函数也是一种数据类型
• 逻辑式：例如SQL、Prolog，代码是逻辑式的，存在判断

编程语言没有改变很多，但是编程语言所编写的程序变得又大又复杂了。

我们为什么需要静态分析

静态分析可以从程序的可靠性、安全性、编译优化、程序理解方面解决下面问题：

• 可靠性问题

  程序可能存在的内存泄露，空指针等

• 安全性问题

  敏感信息泄露，注入攻击等。

• 编译优化问题

  死代码优化、code motion

• 程序理解

  IDE调用关系逻辑、类型提示等

静态分析是什么

我想在运行一个程序P之前，就了解P程序所有的行为。

• P存在信息泄露吗？
• P存在空指针引用吗？
• P程序的cast类型是安全的吗？
• P程序V1和V2会指向同一块内存地址吗？
• 代码是否是死代码？
• ……

其实，并不存在一个方法能够准确的告诉你这些情况。如果你的程序是由递归可枚举语言（现在主流编程语言）编写的程序，它的non-trivial property都是不可判断的。

non-trivial property: interesting properties / the properties related with run-time behaviors of programs.

总而言之：一个完美的，判断程序所有行为的检测方法是不存在的。一个完美的静态分析方法是满足既Sound有Complete的结果。

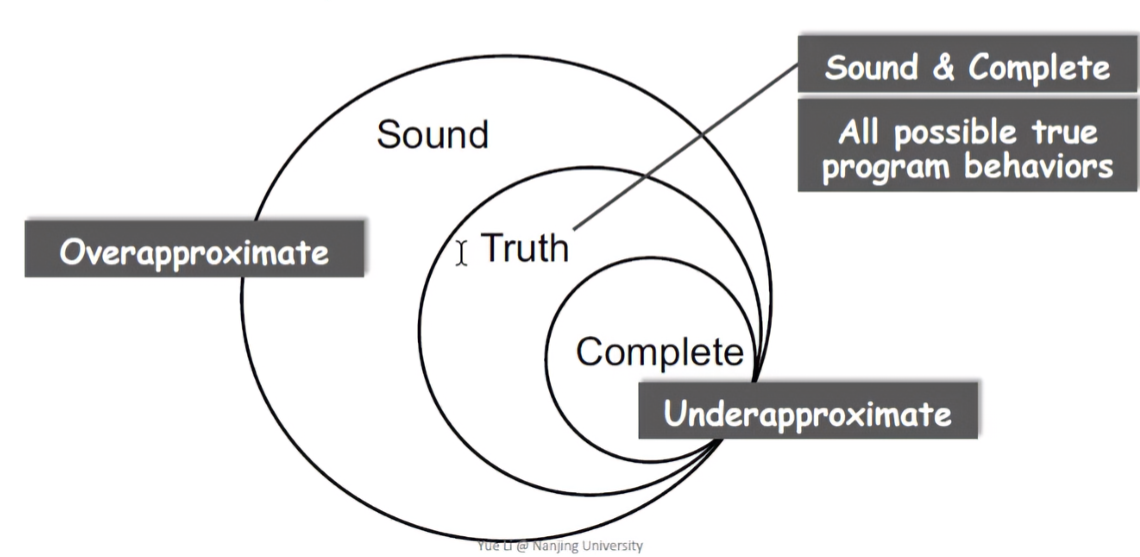
在上图里，Truth表示事实上程序存在的漏洞数，即程序所有可能的行为。Complete和Sound可以简单理解成无误报（False positives）有漏报（False negatives），有误报无漏报：

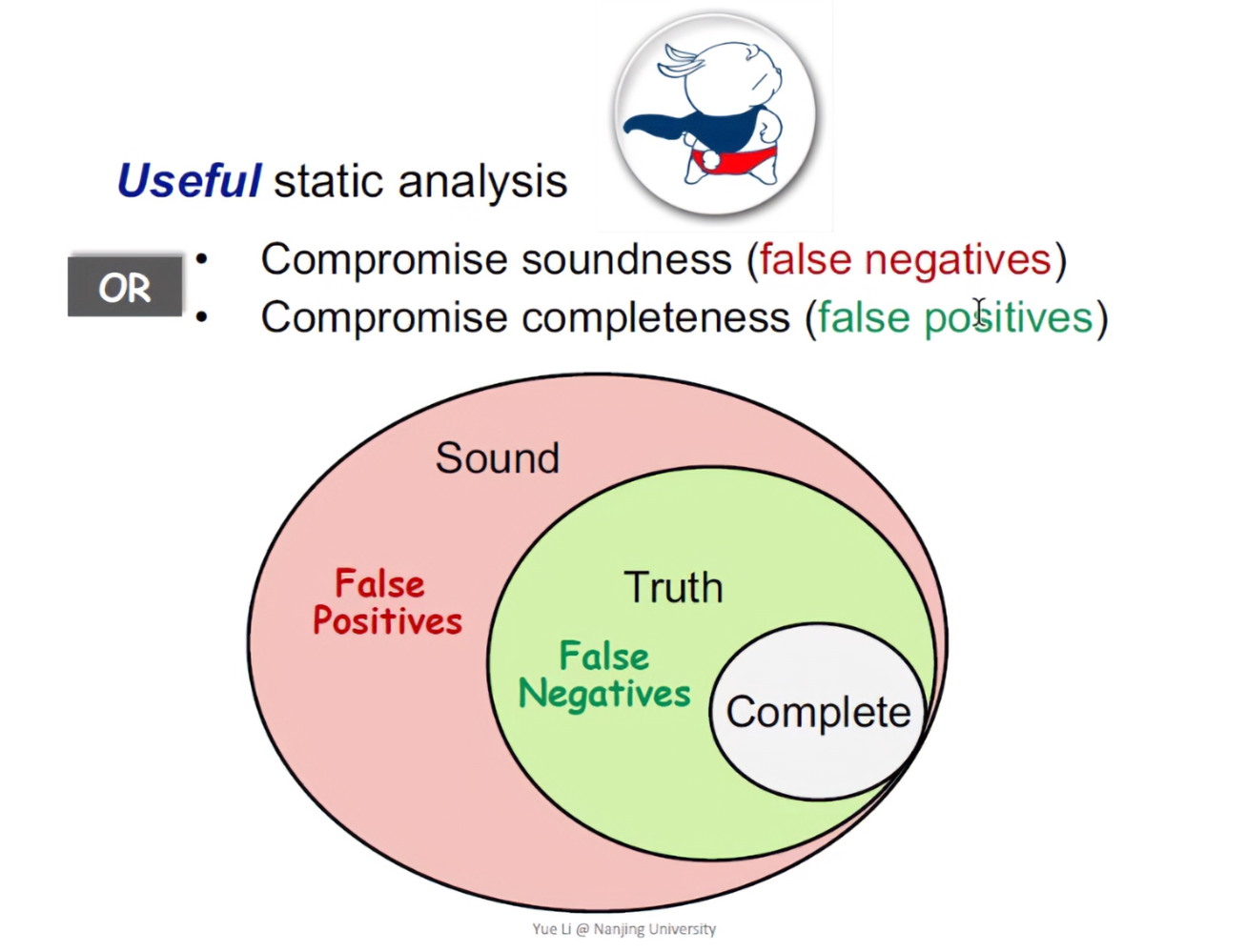
妥协Soundness会带来漏报，妥协Completeness会带来误报。**在真正的程序当中，绝大部分程序都是妥协Completeness。**也就说分析的话，尽可能地Sound（即妥协Completeness）。Soundness对一类的静态分析应用是缺一不可的。

如上图，如果一个静态分析不是Soundness的话，那在实际分析的过程中，可能只沿着a.fld = b; -> B b' = (B) a.fld;这条路径，从而判断cast语句（强制类型转换）是安全的。但如果是Sound，会判断另一条C的路径，会得出Cast是不安全的结论。

从下面的伪代码示例，我们可以高屋建瓴地了解静态分析：

# 从静态分析的角度，判断X等于？
	if (input)
		x = 1;
	else
		x = 0;
->	x= ?

# Answer:

1. when input is true, x = 1
   when input is false, x = 0 √符合complete
特点：Sound, precise, expensive

2. x = 1 or x = 0 √符合sound
特点：Sound, imprecise, cheap

3. x = 1 or x = 0 or x = 3 √符合sound，但存在误报

4. x = -1 or x = 0 ×不符合sound，因为没有x = 1，存在漏报和误报

一句话概括静态分析：在保证Soundness（无漏报或许有误报）的情况下，在分析的精度和速度上做一个有效的平衡。

Intermediate Representation（中间表示）

Complier

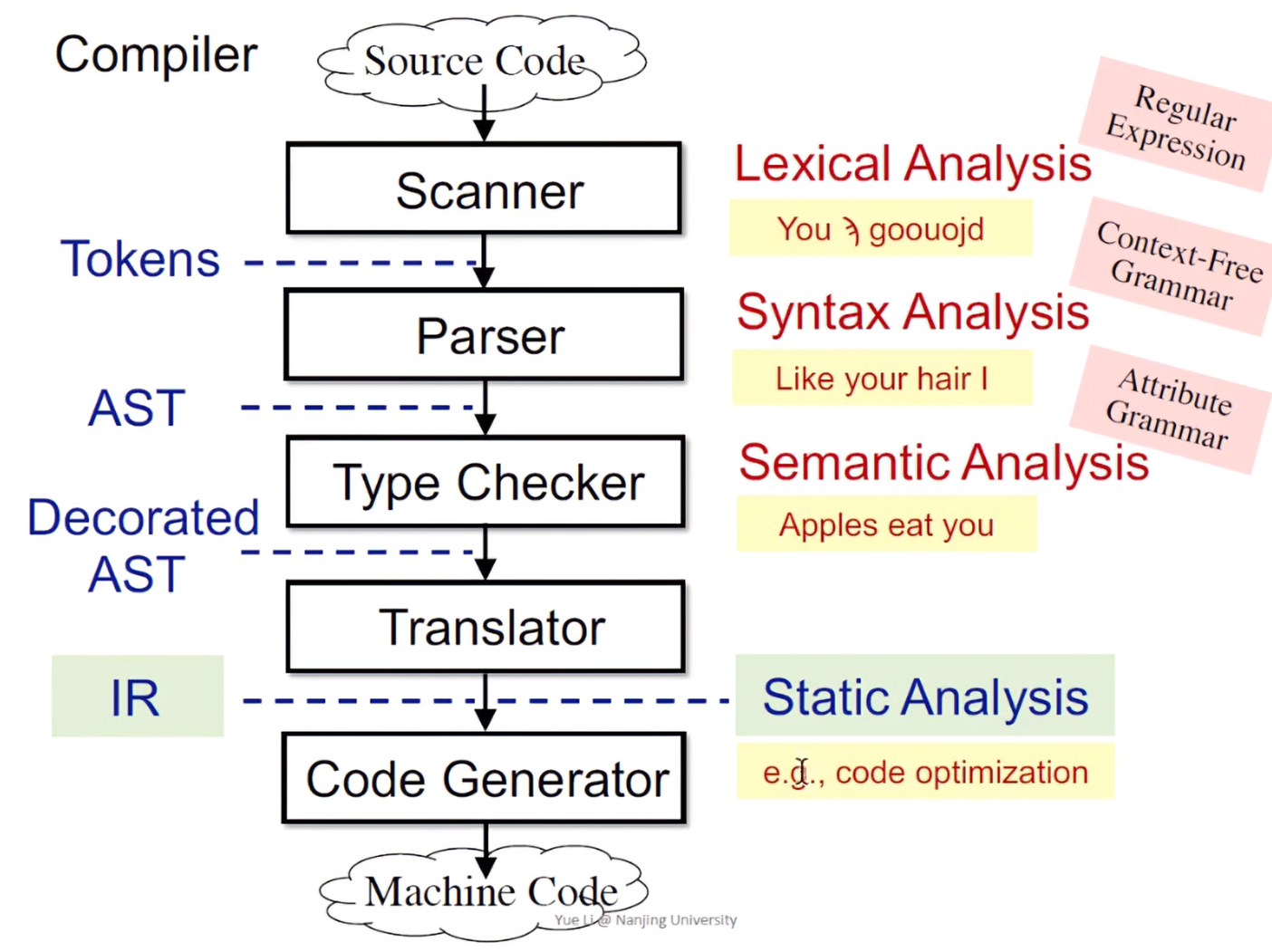
编译器会对源码进行词法分析（Scanner），判断每个单词是否是合理的，如果是合理的，则会对每个单词生成一个tokens，移交语法分析器（Parser）进行分析；tokens的语法符合规则（Context-Free Grammar），会将程序转换成抽象语法树，代码成为一个树的结构；下一步交由类型检查（Type Checker），判断是否存在类型错误，类型检查的语义通过后，会生成Decorated AST；如果代码还需要做后续的优化，编译器会通过Translator中间转换器，将DAST转换成中间形式三地址码（IR，Intermediate Representation），最后交给Code Generator生成机器可执行的代码。

AST vs. IR

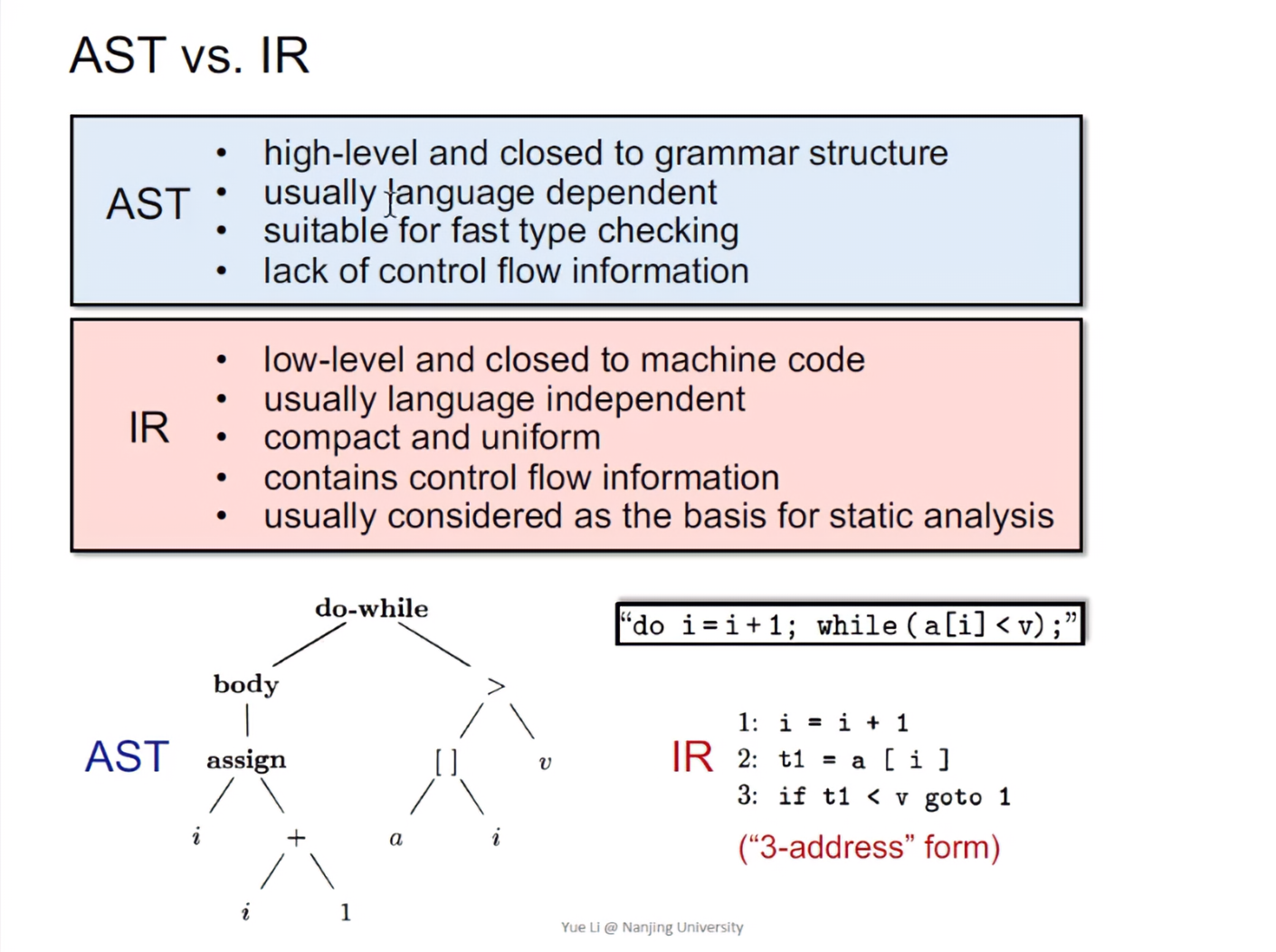
其中最重要的一点是：不依赖编程语言的三地址码，通常会作为程序分析过程中，正统的中间表示。

三地址码包含控制流信息，更利于静态分析。正是这个特性，让三地址码优于抽象语法树，作为静态分析的基础。

3-Address Code（3AC）

There is at most one operator on the right side of an instruction.

				|	t1 = a + b
a + b + 3 - >	|
				|	t2 = t1 + 3

三地址码转换会引入临时变量，这里就是将a+b的值给t1，然后t1+3给t2。

为什么叫三地址码？

这是一种概念上的说法，地址并非传统意义上的地址，按照上面的例子，三地址如下：

1. 变量名字：a,b
2. 常量：3
3. 临时变量：t1,t2

三地址码整体理解只是一种中间表示形式，转换之后右侧每个式子最多只有一个操作符。

常见的三地址码形式

• x = y bop z
• x = uop y
• x = y
• goto L - 无条件跳转
• if x goto L - 有条件跳转
• if x rop y goto L

x, y, z：地址

bop：二元操作符，可以是运算符，比如加减运算，或是逻辑运算（与或非）

uop：一元操作符，unary opertaion(minus, negation, casting)，负值，取反，类型转换

L：代表一个程序/函数的地址

rop：关系操作符，大于、小于、等于等等

Soot and Its IR：Jimple

Jimple是Soot静态分析器的三地址码，以下面的几段代码为示例，简单分析Soot实际分析过程中所产生的三地址码。

For循环：

/* For LOOP JAVA Source code*/
package nju.sa.examples;
public class ForLoop3AC {
	public static void main(String[] args){
		int x = 0;
		for(int i = 0; i < 10; i++){
			x = x + 1;
		}
	}
}

/* 3AC (jimple) */
public static void main(java.lang.String[]){
    java.lang.String[] r0; 
    int i1; 
    r0 := @parameter0: java.lang.String[]; // r0即传参后的值
    i1 = 0; // for循环的i
 
    //这里x是不应该被优化掉的，可能是前端的一些选项导致了x被优化
    
    lable1:
    	if i1 >= 10 goto label2; //不满足循环条件跳出循环
    	i1 = i1 + 1;
    	goto label1; //直到i1>=10，否则一直在循环
   	
    label2:
    	retrun;   	
}

Do-While：

/* Do-While JAVA Source code*/
package nju.sa.examples;
public class DoWhile3AC {
	public static void main(String[] args){
		int[] arr = new int[10];
        int i = 0;
        do{
            i = i + 1;
        } while(arr[i] < 10);
	}
}

/* 3AC (jimple) */
public static void main(java.lang.String[]){
    java.lang.String[] r0; 
    int[] r1;
    int $i0, i1;
    
    //$i0只是临时变量的意思，等同于_i0或i0
    
    r0 := @parameter0: java.lang.String[]; // r0即传参后的值
    r1 = newarry (int)[10]
    i1 = 0; 
 
    lable1:
    	i1 = i1 + 1;
    	$i0 = r1[i1]
		if $i0 < 10 goto label1;
		return;
}

Call：

/* Method Call JAVA Source code*/
package nju.sa.examples;
public class MethodCall3AC {
	
    String foo(String para1, String para2){
        return para1 + " " + para2;
    }
    
    public static void main(String[] args){
        MethodCall3AC mc = new MethodCall3AC();
        String result = mc.foo("Hello","World");
    }
}

/* 3AC (jimple) */
java.lang.String foo(java.lang.String, java.lang.String){
    nju.sa.examples.MethodCall3AC r0;
    java.lang.String r1, r2, $r7;
    java.lang.StringBuilder $r3. $r4, $r5, $r6;
    
    r0 := @this: nju.sa.examples.MethodCall3AC;
    r1 := @parameter0: java.lang.String;
    r2 := @parameter0: java.lang.String;
    $r3 = new java.lang.StringBuilder;
    
    // jvm里的四种方法调用
    // invodespecial -> 调用constructor构造函数，还可以调用父类里面的method，调用私有方法
    // invokevirutal -> 常用的方法调用, instance methods call，虚拟派发 
    // invokeinterface -> 和上面调用很像，但不做优化，会检查方法Interface是否都实现
    // invokestatic -> 调用静态方法
    // Java7之后还有一个 invokedynamic -> 作为动态语言跑在jvm上？
    
    specialinvoke $r3.<java.lang.StringBuilder: void <init>()>();
    
    // Method Signature <java.lang.StringBuilder: void <init>()>
    // 包含声明所在的类名：如果有返回值，会有返回值的类型，一般情况下还会包含方法名字（参数1 类型1，参数2, 类型2）
    
    $r4 = virtualinvoke $r3.<java.lang.StringBuilder: java.lang.StringBuilder append(java.lang.String)>(r1);
    //调用$r3.<java.lang...>的方法的参数是r1
    
    $r5 = virtualinvoke $r4.<java.lang.StringBuilder: java.lang.StringBuilder append(java.lang.String)>(" ");
    $r6 = virtualinvoke $r5.<java.lang.StringBuilder: java.lang.StringBuilder append(java.lang.String)>(r2);
    $r7 = virtualinvoke $r6.<java.lang.StringBuilder: java.lang.StringBuilder append(java.lang.String)>(r2);
    
    return $r7;
}

public static void main(java.lang.String[]){
    java.lang.String[] r0;
    nju.sa.examples.MethodCall3AC $r3;    
    
    r0 := @parameter0: java.lang.String[];    
    $r3 = new nju.sa.examples.MethodCall3AC;
    
    specialinvoke $r3.<nju.sa.examples.MethodCall3AC: void <init>()>();
    
    virtualinvoke $r3.<nju.sa.examples.MethodCall3AC: java.lang.String foo(java.lang.String,java.lang.String)>("Hello","World");
}

Class：

/* Class JAVA Source code*/
package nju.sa.examples;
public class Class3AC {
	
	public static final double pi = 3.14;
    public static void main(String[] args){
        
    }
}

/* 3AC (jimple) */
public class nju.sa.examples.Class3AC extends java.lang.object{
    public static final double pi;
    
    public void <init>(){
        
		nju.sa.examples.Class3AC r0;
        
        r0 := @this: nju.sa.examples.Class3AC;
        
        specicalinvoke 30.<java.lang.object: void <init>()>();
        
        return;
   
    }
    
    public static void main(java.lang.String[]){
        
        java.lang.String[] r0;
        
        r0 := @parameter0: java.lang.String[];
        
        return;
    }
    
    //clinit = class instance / class load init
    public static void <clinit>(){
        
        <nju.sa.examples.Class3AC: double pi> = 3.14;
        
        return;
    }
}

Static Single Assignment（SSA）

SSA是经典的IR里的一种转换格式，会给每一个定义一个新的名字，然后传播到随后的用法（Propagate fresh name to subsequent uses），并且每个变量实际上只有一种定义：

如果经过了一个判断，因为SSA是对每个变量实际只有一个定义，那么会引入φ function进行处理：

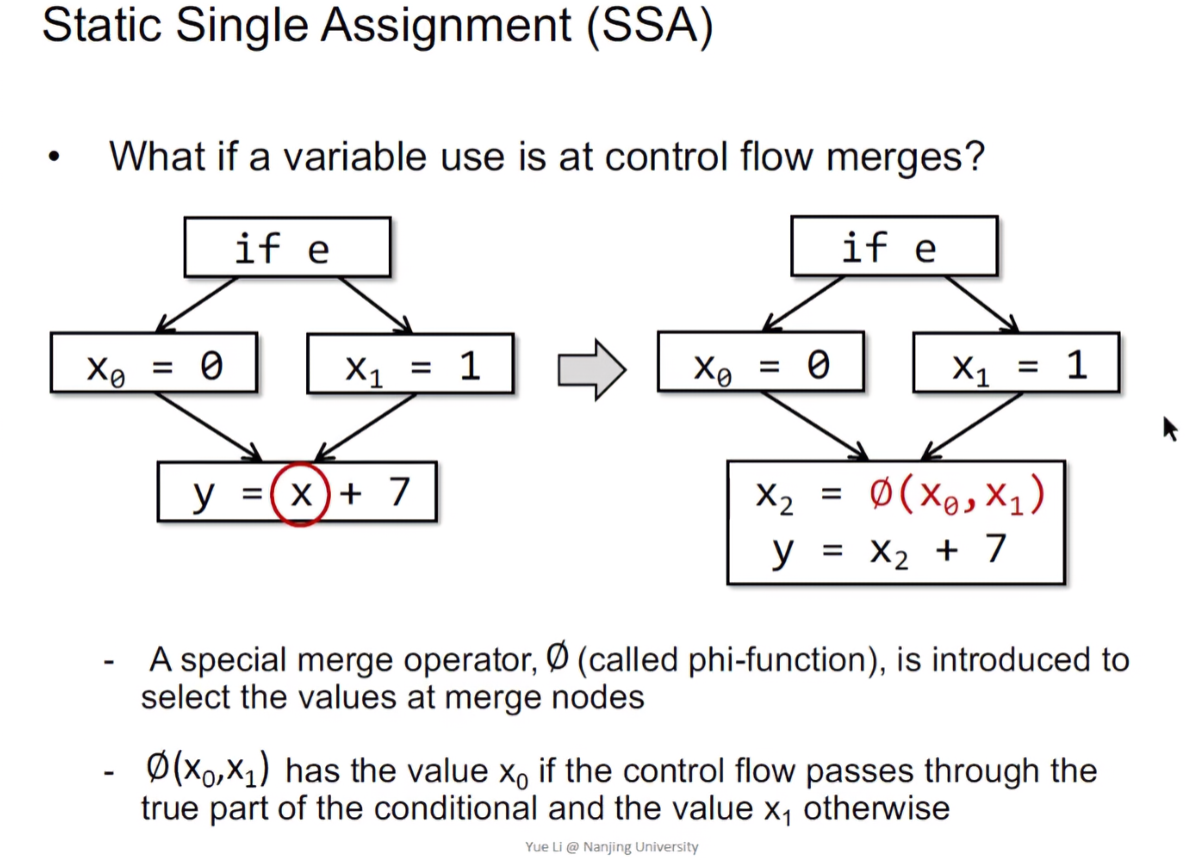
为什么要用SSA？

1. 程序流可以间接地赋值给唯一的变量，这样做的好处就是给一些流程不明显的程序提供一些程序流程上的精度。（May help deliver some simpler analyses, e.g., flow-insensitive analysis gains partial precision of flow-sensitive analysis via SSA）
2. Define-and-Use pairs are explicit. Enable more effective data facts storage and propagation in some on-demand tasks. Some optimization tasks perform better on SSA(e.g., conditional constant propagation, global value numbering) 没看懂，直接放上英文

为什么不用SSA？

1. SSA引入了很多的变量和Φ函数
2. 可能会存在一些性能上的问题

Control Flow Analysis（控制流分析）

控制流分析经常用于作为建立控制流图（CFG, Control Flow Graph）的参考，而CFG又是静态分析的basic structure。CFG中的节点可以是一个单独的三地址码的指令，或一个基本块（BB）。The node in CFG can be an individual 3-address instruction, or (usually) a Basic Block(BB).

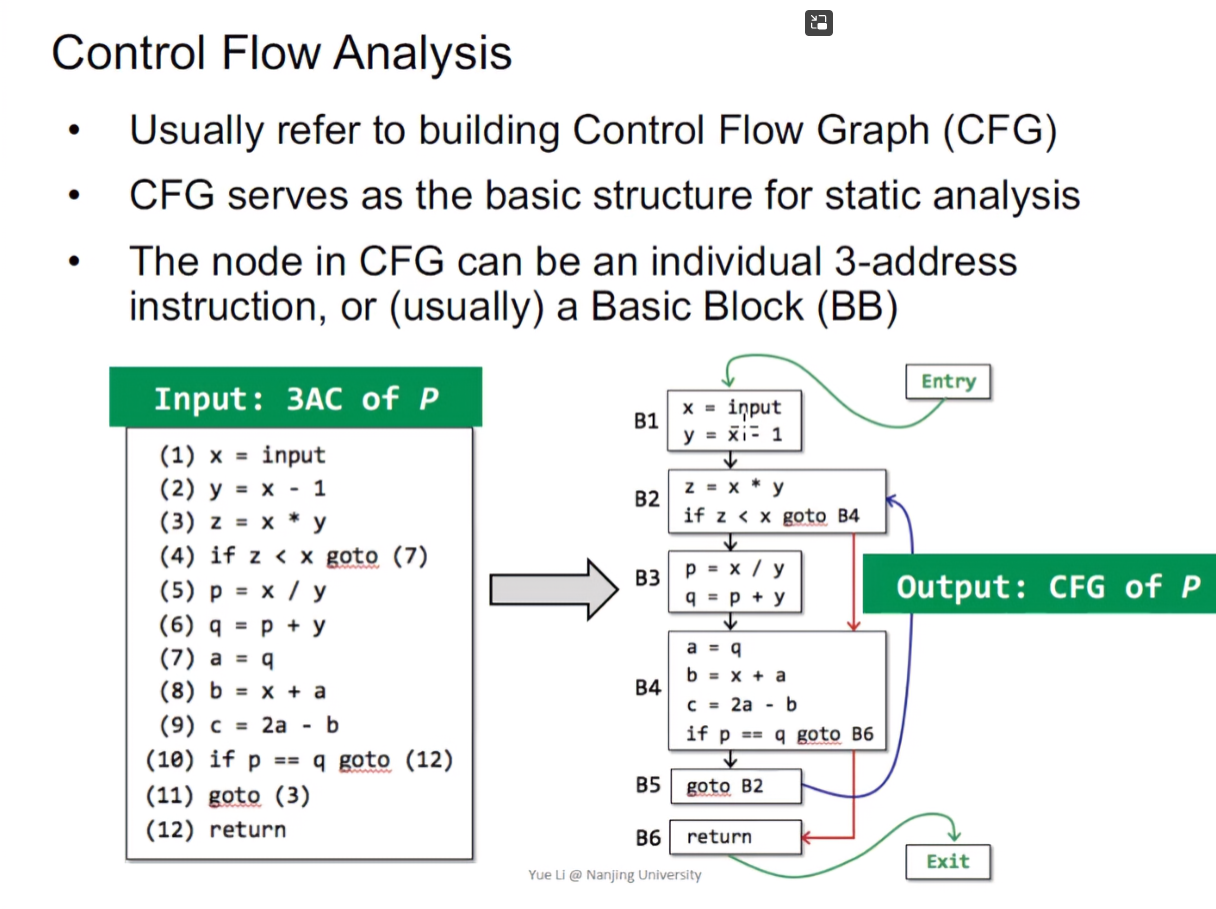
Basic Block（BB）

基本块是满足最多的连续的三地址指令所组成的一个序列。

Basic Block are maximal sequences of consecutive 3-address instructions with the properties that

• It can be entered only at the beginning, i.e., the first instruction in the block.
  • 如果一些指令想成为一个BB，那么这个BB有且只有一个入口，并且这个入口必须是BB的第一个指令
  • 换句话说也就是不存在另一条控制流，走到BB中的第二条或第三条命令
• It can be exited only at the end, i.e., the last instruction in the block
  • BB的出口应该是它最后一个指令
  • 换言之，它的最后一个指令不应该是BB内的中间指令

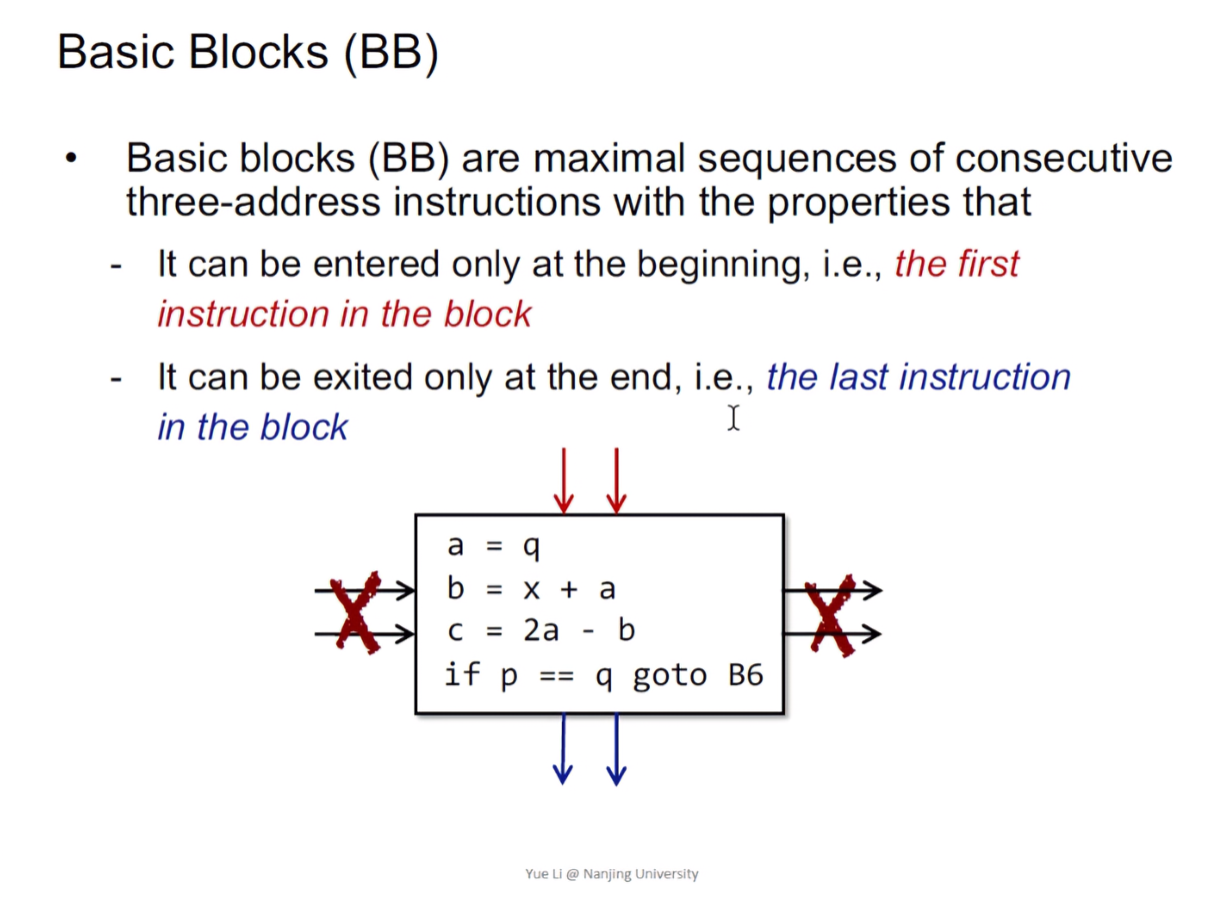
P.S.: IDA里的控制流浏览，一小块一小块的就是BB

如何建立Basic Blocks

INPUT：A sequence of 3-address instructions of P

OUTPUT：A list of basic blocks of P

METHOD：

1. Determine the leaders in P
   1. The first instruction in P is a leader，第一个指令是leader
   2. Any target instruction of a conditional or unconditional jump is a leader，所有GOTO的指令也是leader
   3. Any instruction that immediately follows a conditional or unconditional jump is a leader，GOTO的下一行指令也是leader
2. Build BBs for P
   1. A BB consists of a leader and all its subsequent instructions until the next leader，BB包含一个leader和后续的指令，一直到下一个leader为止。

x = input
y = x - 1
z = x * y
if z < x goto (7)
p = x / y
q = p + y
a = q
b = x + a
c = 2a - b
if p == q goto (12)
goto (3)
return 


// Output: BBs of P
// a:1 b: 3/7/12 c:5/11/12
// leader: 1/3/5/7/11/12

// Build BBs for P
B1 {1,2}
B2 {3,4}
B3 {5,6}
B4 {7,8,9,10}
B5 {11}
B6 {12}

Control Flow Graph（控制流图）

• The nodes of CFG are basic blocks
• There is an edge from block A to block B if and only if，当且仅当存在一条从A到B的边
  • There is a conditional or unconditional jump from the end of A to the beginning of B，有条件和无条件的跳转，从A的结尾指向B的开头
  • B immediately follows A in the original order of instructions and A does not end in an unconditional jump，在原来的指令顺序中，B紧随A，且A没有以无条件跳转的方式结束
• It is normal to replace the jumps to instruction labels by jumps to basic blocks

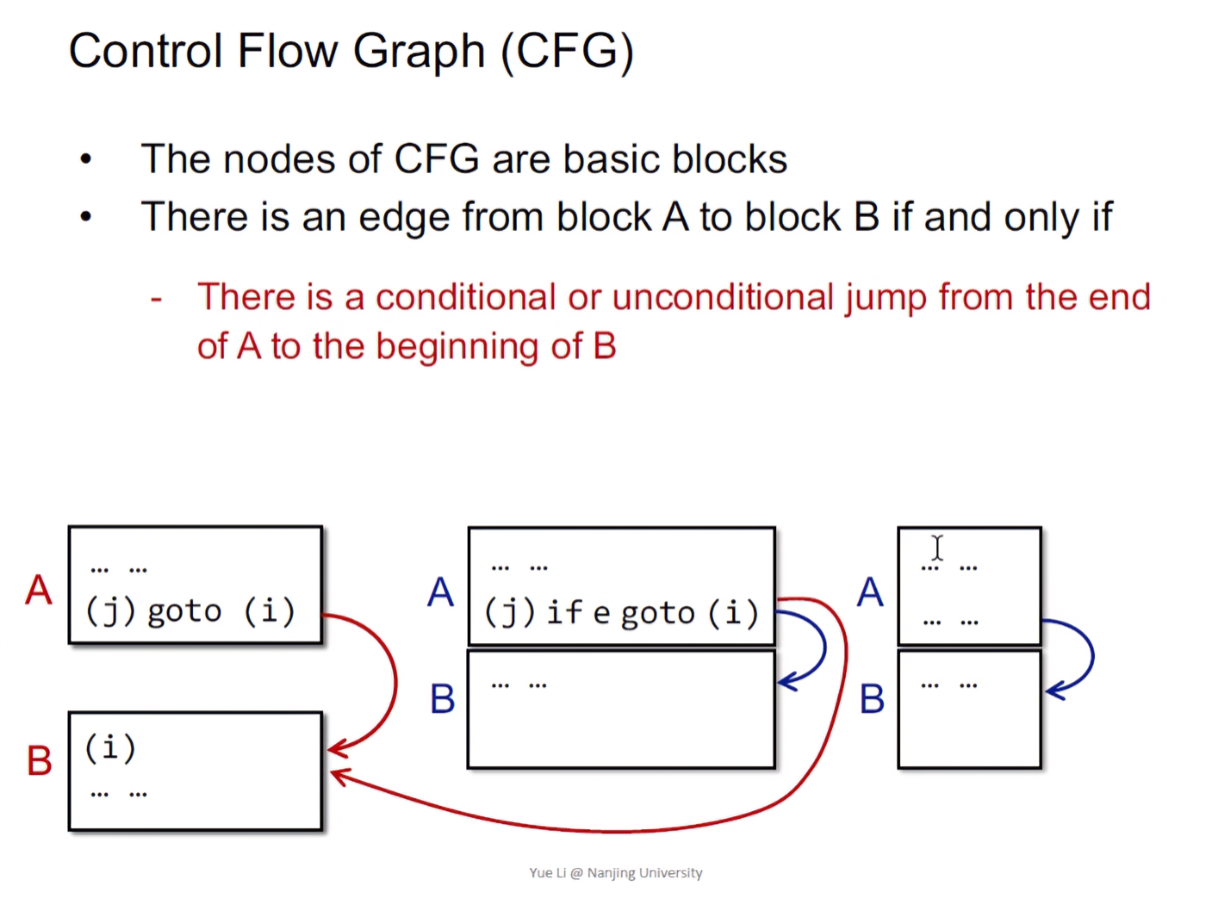
在红A和红B中，因为A里有个无条件跳转，所以应添加边；在蓝A与蓝B中，A存在一个有条件跳转，且满足e时跳转到红B，此时蓝A与蓝B之间也应该添加边，因为要满足Sound的原则，即所有的程序路径都要考虑到，此时如果不满足e时，程序会执行到蓝B的leader（图里蓝A和蓝B是紧挨着的，表示它们的三地址码也是紧接着的），依然是一条执行路径。

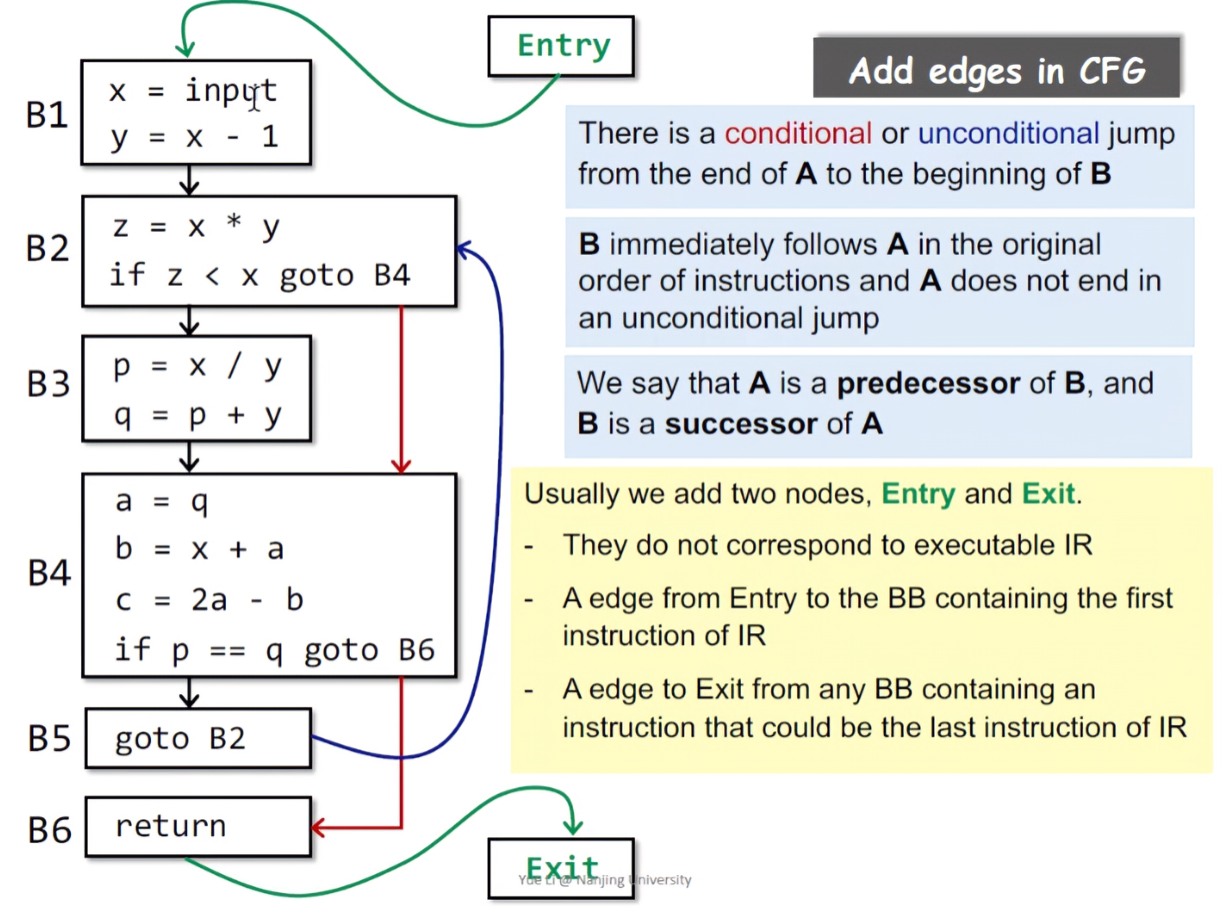
在一个控制流图中，通过BB的出入口可以得到该代码块的前驱节点和后继节点，其中B4的前驱节点包括B3、B2（即该两个BB的出口都是B4），后继节点包括B5（B5的入口是B4的出口）。除此之外，控制流图中还存在入口和出口。实际静态分析的时候，多线程或其他情况下，可能有多个入口（入边）；同样的，出口（出边）也会存在多个。

Data Flow Analysis（数据流分析）

数据流分析是静态分析体系里非常基础的部分，它属于后端编译、优化的一种技术。

Overview of Data Flow Analysis

In each data-flow analysis application, we associate with every program point a data-flow value that represents an abstraction of the set of all possible program states that can be observed for that point.

实际上，静态的数据流分析最后达成的结果，就是给每一个程序的程序点关联一个数据流的值，这个值是程序状态的抽象表达（迭代算法这节中，该值所表达的是Definition reaches的状态）。

也是通过下面的迭代算法的例子，通过不断使用Transfer function来判断是否符合约束规则，来发现一个适应于safe-approximation的状态。

May and Must Analysis

• May Analysis

  • Outputs information that may be true(over-approximation)，输出的信息可能是正确的

• Must Analysis

  • Outputs information that must be true(under-approximation)，输出的信息一定是正确的
  • Over- and under-approximations are both for safety of analysis. 无论是over还是under都是为了让分析的结果更精确。

  基于此，我们可以使用Safe-approximation来描述分析：

  如果这个分析是May Analysis，是绝大多数的分析，那么Safe-approximation的Safe实际上为Over；反之是Must Analysis，是一小部分的分析，那么Safe-approximation的Safe为Under。一般情况下，May Analysis所做操作，会把集合内所有元素并起来；反之Must Analysis会取交集。

Input and Output States

• Each execution of an IR statement transforms an input state to a new output state. 如果一个BB被称为S1，那么它的输入状态，我们可以用IN[S1]表示。相应地，执行完语句之后，程序状态会变为OUT[S1]。
• The input(output) state is associated with the program point before(after) the statement. 程序的输入和输出状态都和程序点相关联，这个程序点一般都是和语句的前和后关联。

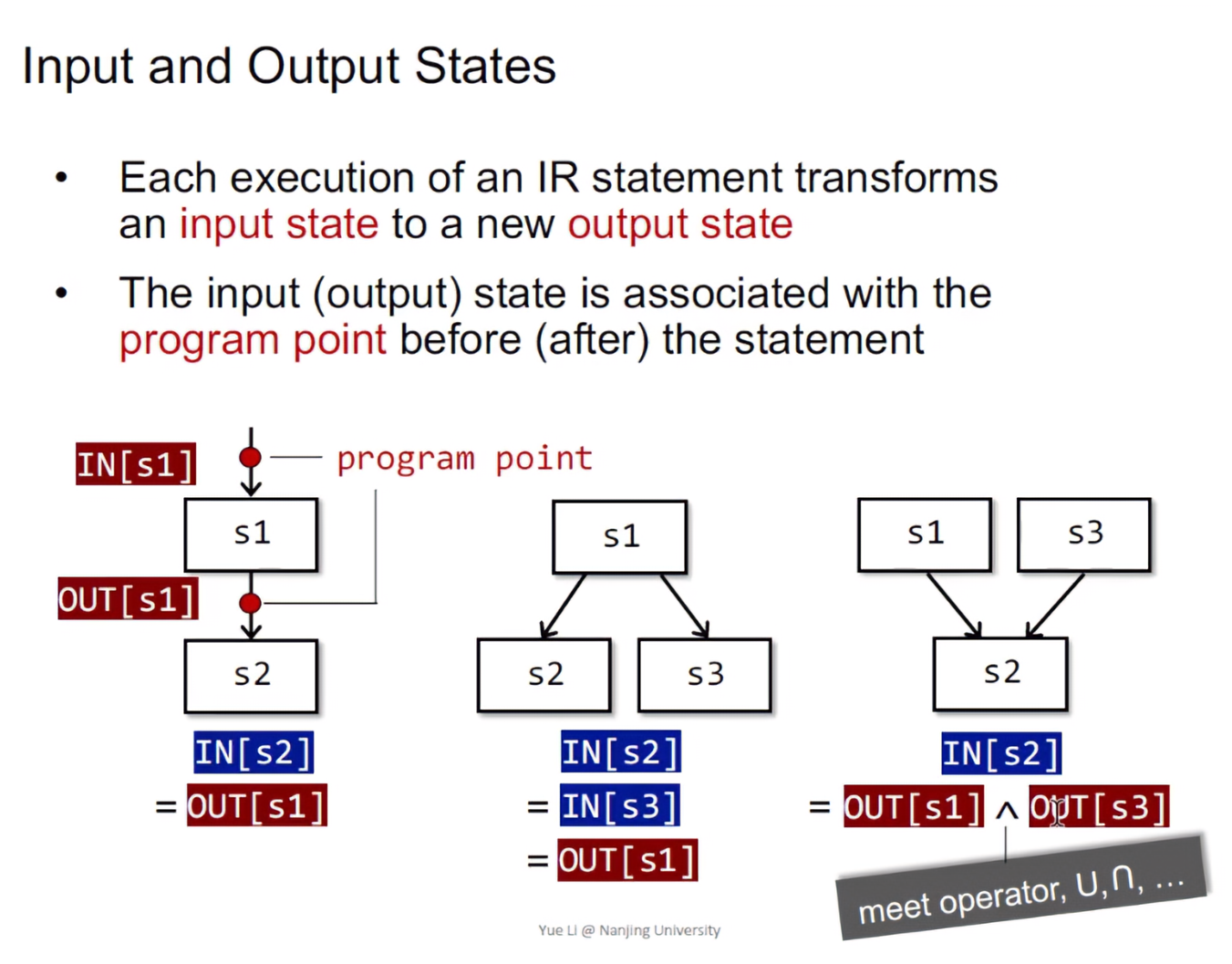
图三中存在meet operator，是指需要将OUT[S1] 和OUT[S2]进行处理，将两个前驱输出处理后的结果作为下个后继的输入。

Notation for Transfer Function’s Constraints

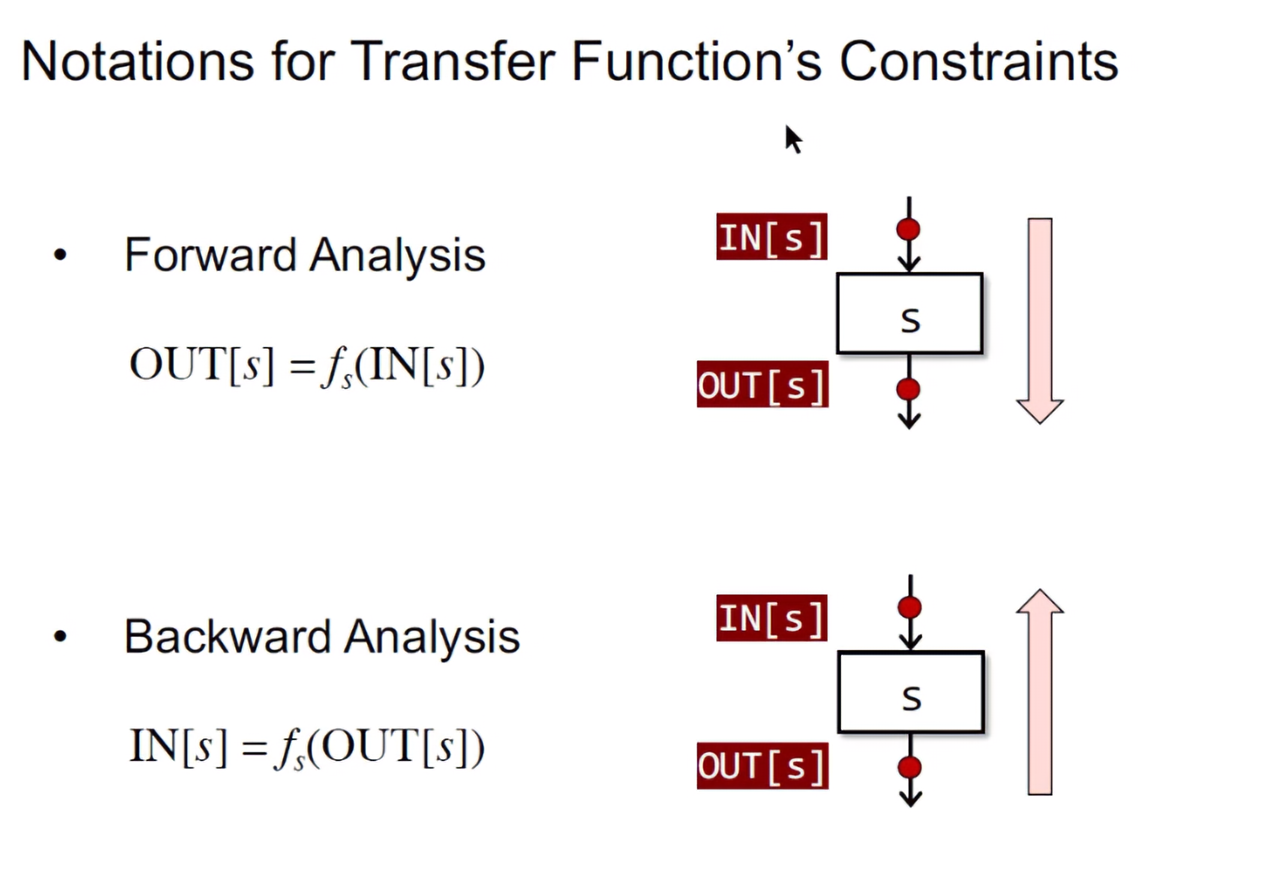
• Forward Analysis
  • OUT[s] = f_s(IN[s])
    • S之前的状态IN[s]，通过传输函数fs，转换成之后的状态OUT[s]
• Backward Analysis
  • IN[s] = f_s(OUT[s])
    • 与前向分析相反，这个是将S之后的状态OUT[s]作为输入，通过转换函数fs，将之前的状态IN[s]作为输出

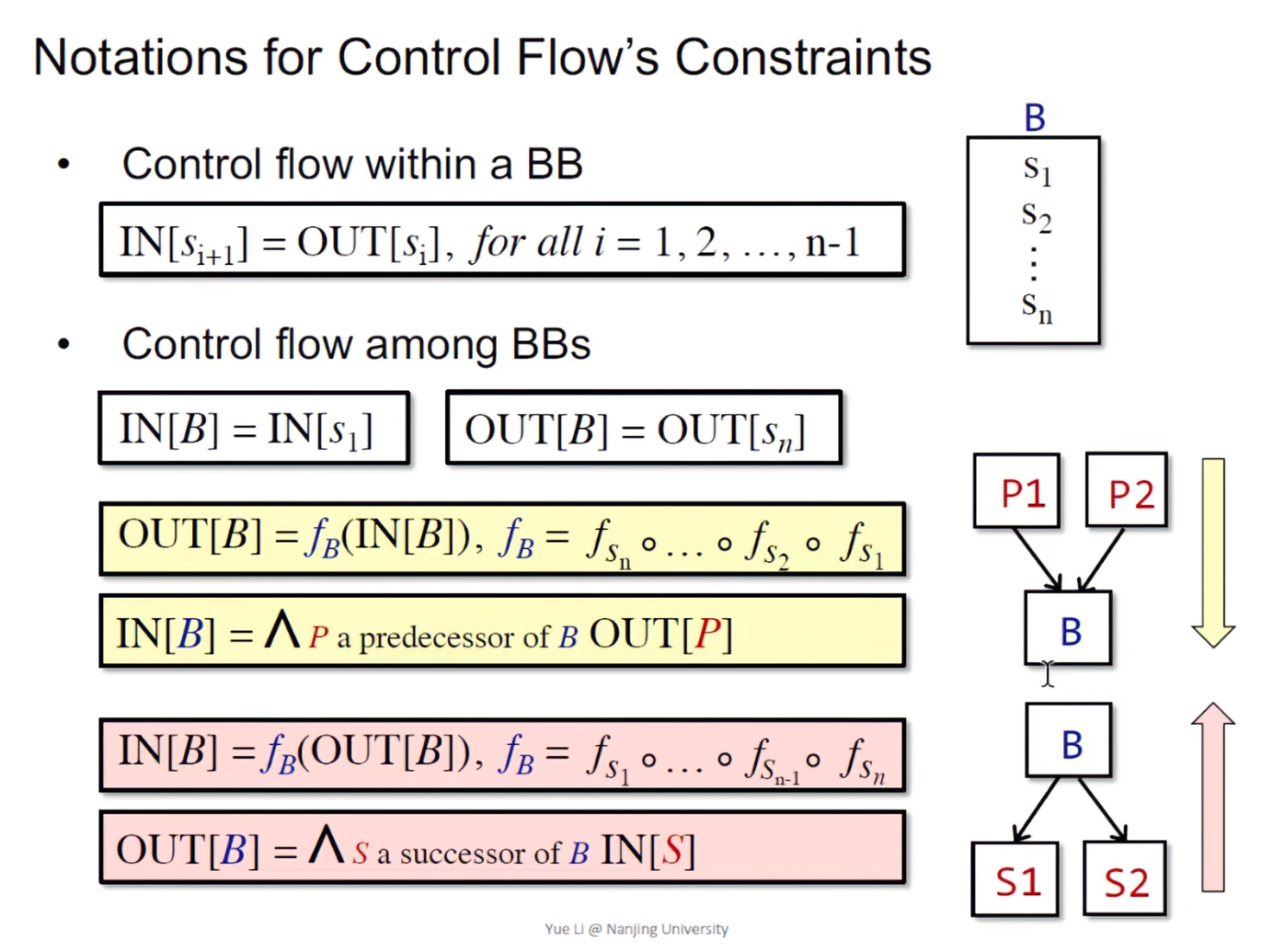
• Control flow within a BB

  • IN[s_i+1] = OUT[s_i]，for all i = 1,2,…,n-1
    • 对于某一个BB的输入状态，是其前驱节点的输出状态

• Control flow among BBs

  • IN[B] = IN[s₁]

    • 对于某一个BB的输入状态，其实就是其第一个语句（leader）的输入状态

  • OUT[B] = OUT[s_n]

    • 同样的，对于该BB的输出状态，就是最后一个语句的输出状态

  • OUT[B] = f_B(IN[B])，f_B = f_sn · … · f_s2 · f_s1 （Forward Analysis）

    • 一个BB的传输函数的表示，就是里面每一个对应的传输函数的处理

  • IN[B] = ^ P a predecessor of B OUT[P]

    • The meet operator ^ is used to summarize the contributions from different paths at the confluence of those paths.
    • B的输入则是它所有的前驱的输出，通过一定的处理，作为B的输入

  • IN[B] = f_B(OUT[B])，f_B = f_s1 · … · f_sn-1 · f_sn （Backward Analysis）

  • OUT[B] = ^ S a predecessor of B IN[S]

    • B的输出就是其所有后继的输入状态

Reaching Definitions Analysis

Issues Not Covered（本节不会涉及到的问题）

• Method Calls
  • Intra-procedural CFG（跨函数控制流图）
  • Will be introduced in lecture: Inter-procedural Analysis（跨函数分析）
• Aliases
  • Variables have no aliases（两个变量同时指向一个内存地址，此时称这两个变量互为别名关系）
  • Will be introduced in lecture: Pointer Analysis（指针分析）

Reaching Definitions

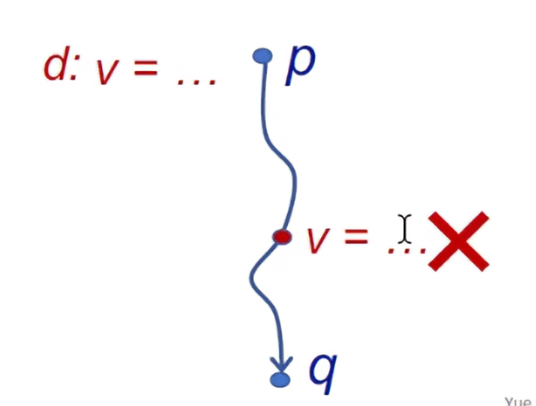
A definition d at program point p reaches a point q if there is path from p to q such that d is not “killed” along that path.

• A definition of a variable v is a statement that assigns a value to v.
  • 假设有一个定义v的变量，那么这个定义用d来表示。
• Translated as: definition of variable v at program point p reaches point q if there is a path from p to q such that no new definition of v appears on that path.
  • 在p里存在一个定义d，也就是有一个定义v的变量。那么从p到达q的程序路径中，不能够让v被重新定义（或存在v新的定义）。

• Reaching definitions can be used to detect possible undefined variables. e.g., introduce a dummy definition for each variable v at the entry of CFG, and if the dummy definition of v reaches a point p where v is used, then v may be used before definition(as undefined reaches v)
  • Reaching definitions 可以用来检测一个变量是否被定义。CFG可以有一个假的入口（因为CFG可以有多个入口，这个假的入口实际上没有被执行），此时引入一个没有被定义的变量，那么在变量v定义的代码块p执行之前，v都处于没有定义的状态。如果静态分析的时候发现，一直处于未定义状态的v，其未定义状态能够一直流入到要用的地方（也就是p），这就意味着v通过一条没有被初始化的路径。
  • 这是一个may analysis，因为实际上还存在别的路径上，变量v存在初始化的可能。

Understanding Reaching Definitions

• Data Flow Values/Facts

  • The definitions of all the variables in a program
  • Can be represented by bit vectors
    • 假如程序有100个定义，那么我们可以用D1, D2, D3, …, D100来表示

• Transfer Function

  • D: v = x op y
    • 这个状态产生了一个关于v的定义D，并且就可以删除掉程序中，其他的关于v的定义。在这个过程中只删除v，对x和y没有影响。
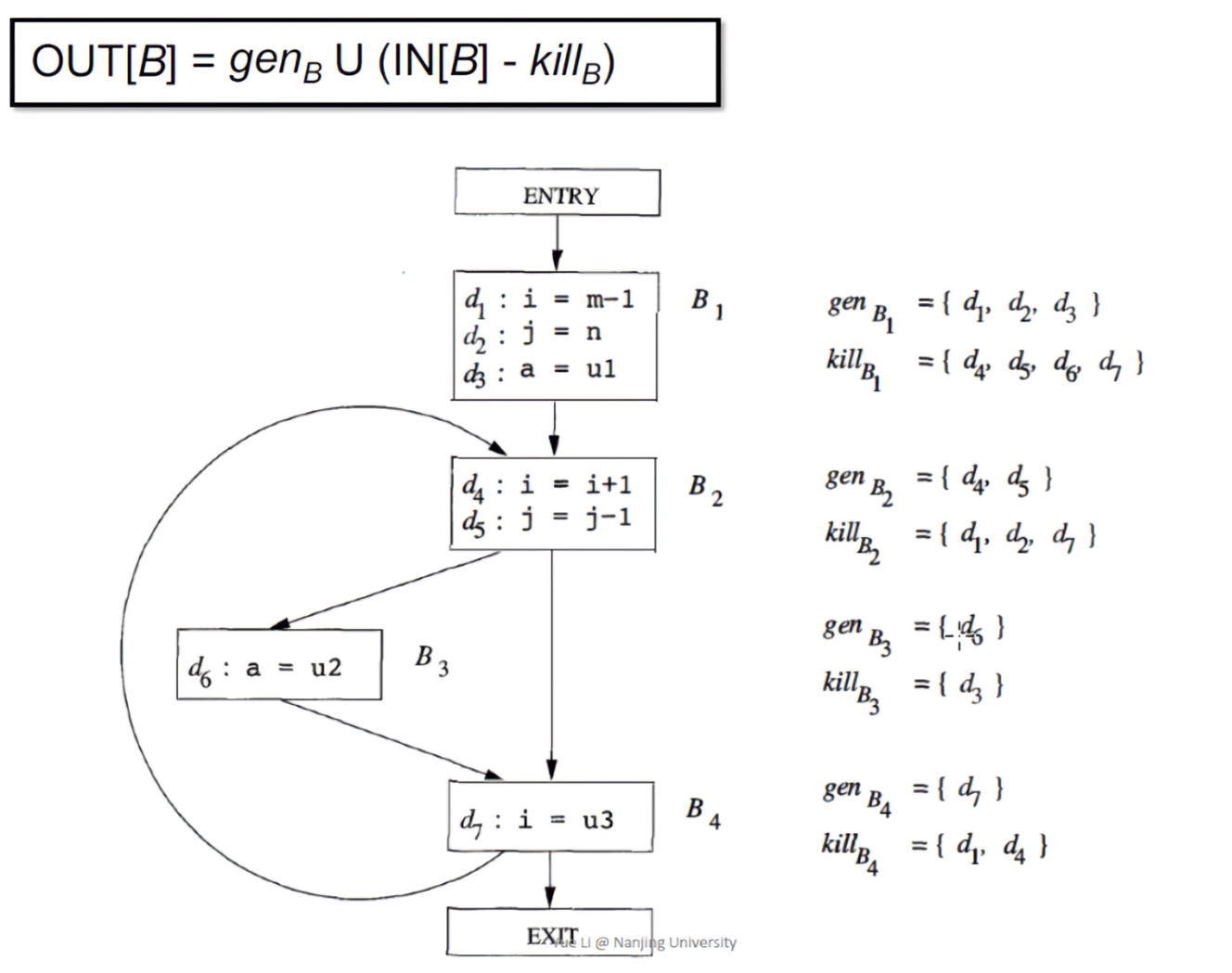
  • OUT[B] = gen_B∪(IN[B]-kill_B)
    • 进入B的定义，并v的重复定义，之后并上自身的定义D，就是B的转换函数。

关于*kill_B*范围的一些想法（个人，非官方）：

由于并不知道控制流图里准确的逻辑关系，所以可能存在一个BB成为B的前驱节点。并且在静态分析的过程中，kill掉后面的定义是没有关系的，因为在代码执行的时候，后面会重新定义；但如果不kill，从后面流入到前面的路径就会出现问题。

• Control Flow
  • IN[B] = ∪_{P a predecessor of B} Out[P]
    • A definition reaches a program point as long as there exists at least one path along which the definition reaches.
    • 这里的并集是指，所有到达B结果的并集。也就是说，只要至少存在一条Definition reach的路径，那么就会有一个Definition reach到达程序点。

Algorithm of Reaching Definitions Analysis（定义到达算法）

Input: CFG(kill_B and gen_B computed for each basic block B)

Output: IN[B] and OUT[B] for each basic block B

METHOD:

entry没有statement，是一个虚拟的，可以看作哨兵元素。因为没有状态，所以没有定义，故为空；对于每一个BB（排除掉entry），它的输出状态都为空。因为这个算法是适用于绝大多数的分析，在有的基本块的entry中，它的初始化状态并非为空，所以此时要排除掉entry。一般情况下，may analysis初始化状态都为空。

初始化结束之后，对于每一个BB，存在一个改变的输出状态，就执行这个循环。对每个BB（同样排除entry）使用转换函数。

那么这个算法会停下来吗？

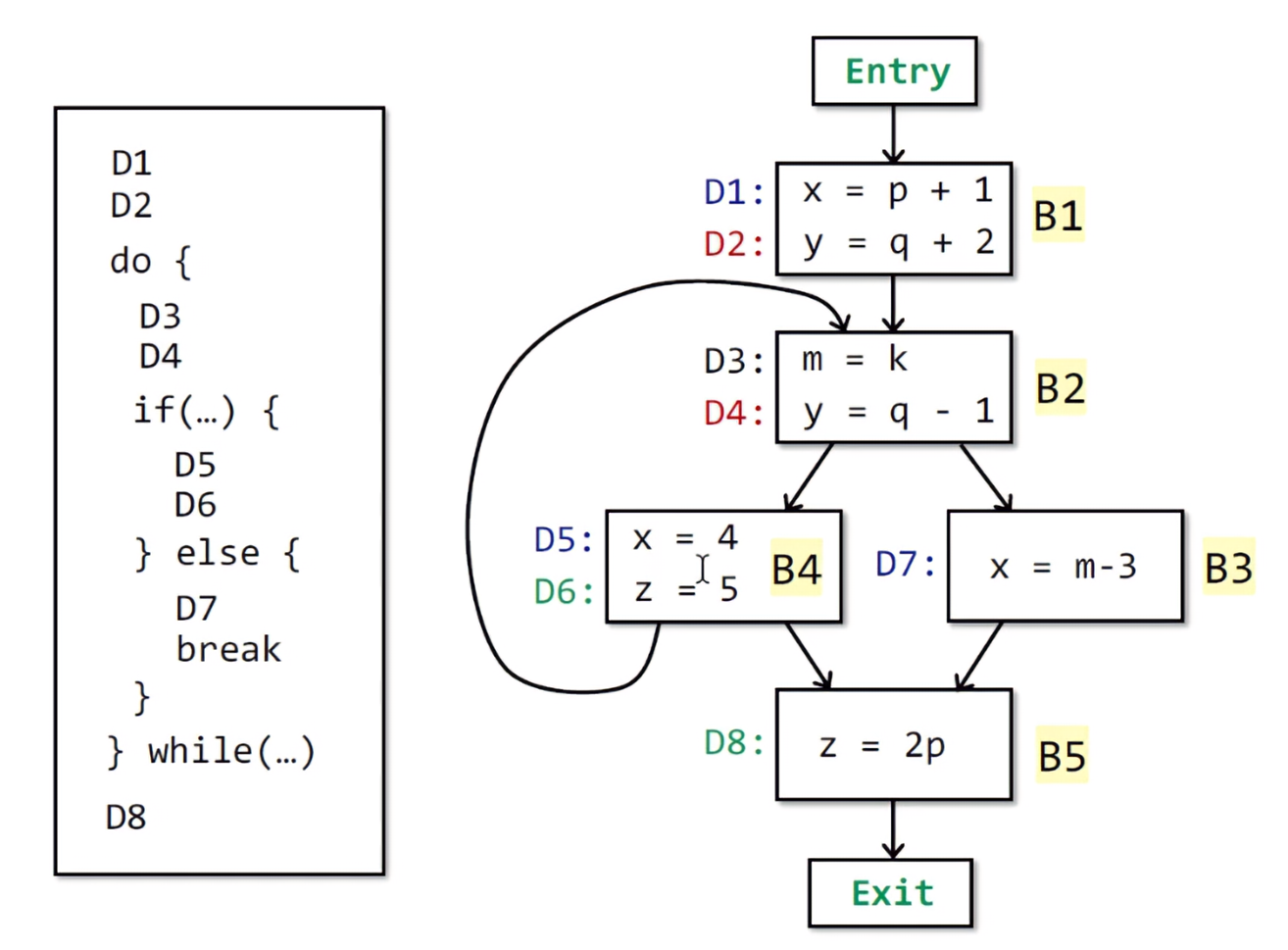
在上面的例题中，我们给每一个定义D建立了一个位向量（bit vector）。因为这里有8个定义，所以这个CFG的Definition Reaches的位向量就是八位。0代表这个定义不能被该向量到达，1代表可以被到达。

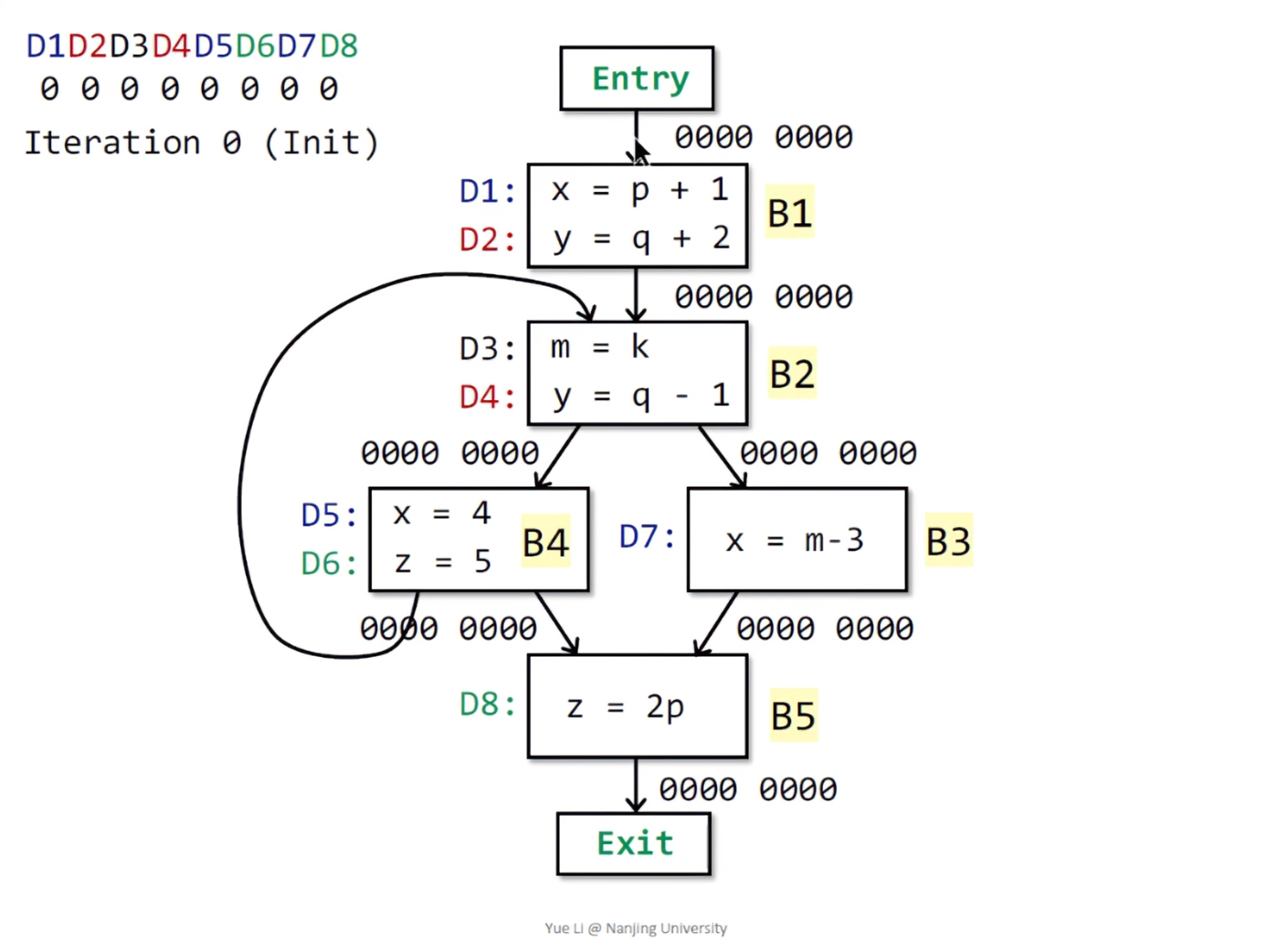
根据算法，所有的BB的输出状态都会被置空。 如果有out被改变，就进行转换函数的迭代。执行完B1后，x和y均被定义，也就是说已经到达了D1和D2，此时位向量的状态就变成了1100 0000。

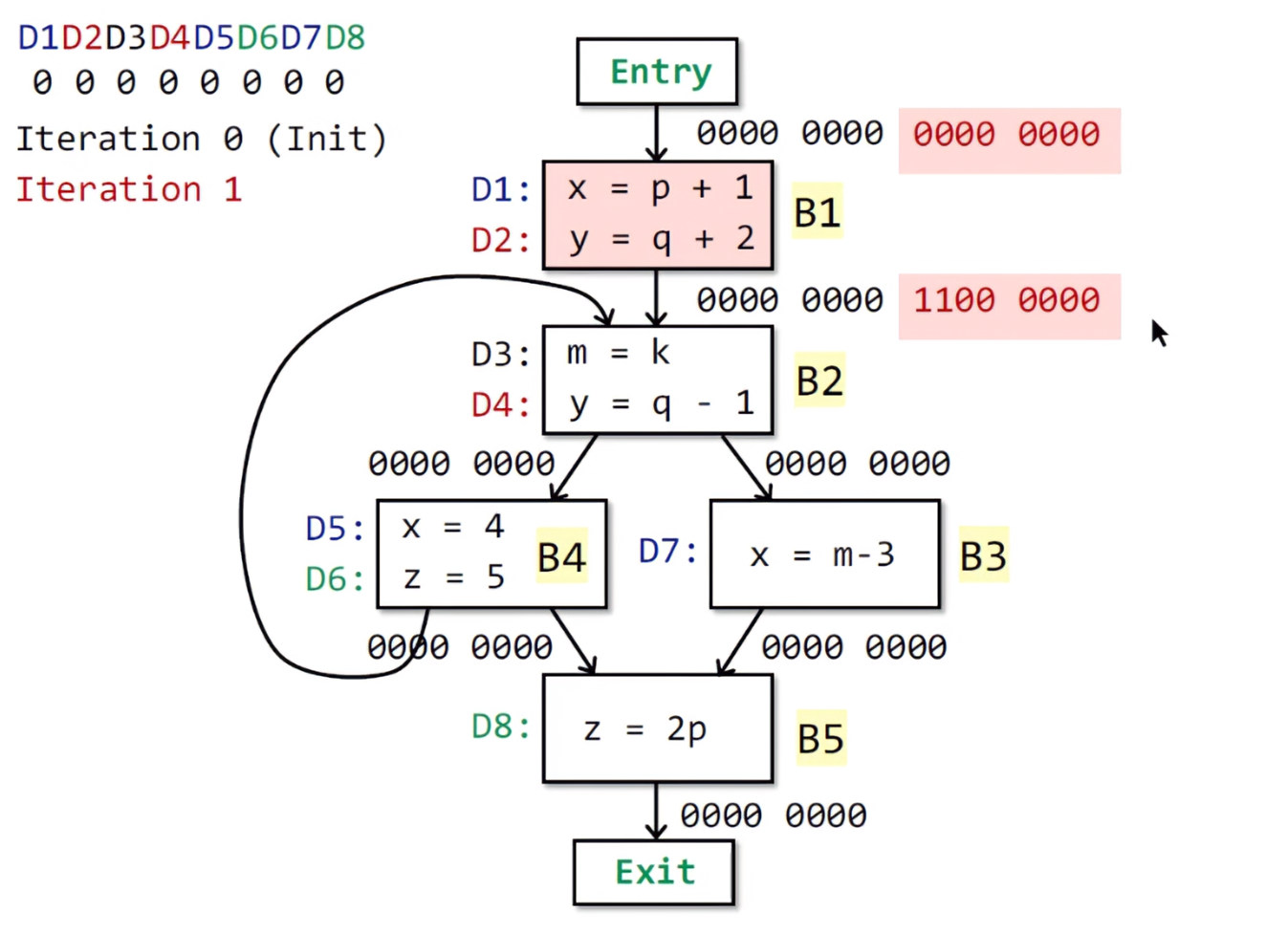
现在开始执行B2，由于

$$IN[B] = ∪_{P\ a \ predecessor \ of \ B} \ Out[P]$$

也就是B2的输入状态，为所有前驱节点输出状态的UNION（并集）。这里B2的前驱节点为B1和B4，B1的输出状态OUT[B1]上面已经得出为1100 0000，而B4[OUT]为初始化的0000 0000。此时进行合并之后（对应位做与运算），得到B2的输入1100 0000。之后来到下一步：

$$OUT[B] = gen_B ∪ (IN[B] - kill_B)$$

而gen_b不难得出，D3中的m被到达，此时由0变1；而D4中的y，由于前驱节点B1中，存在D2重复定义y，需要被kill掉D2，故将第二位置0。所以最后的OUT[B2]为1011 0000。

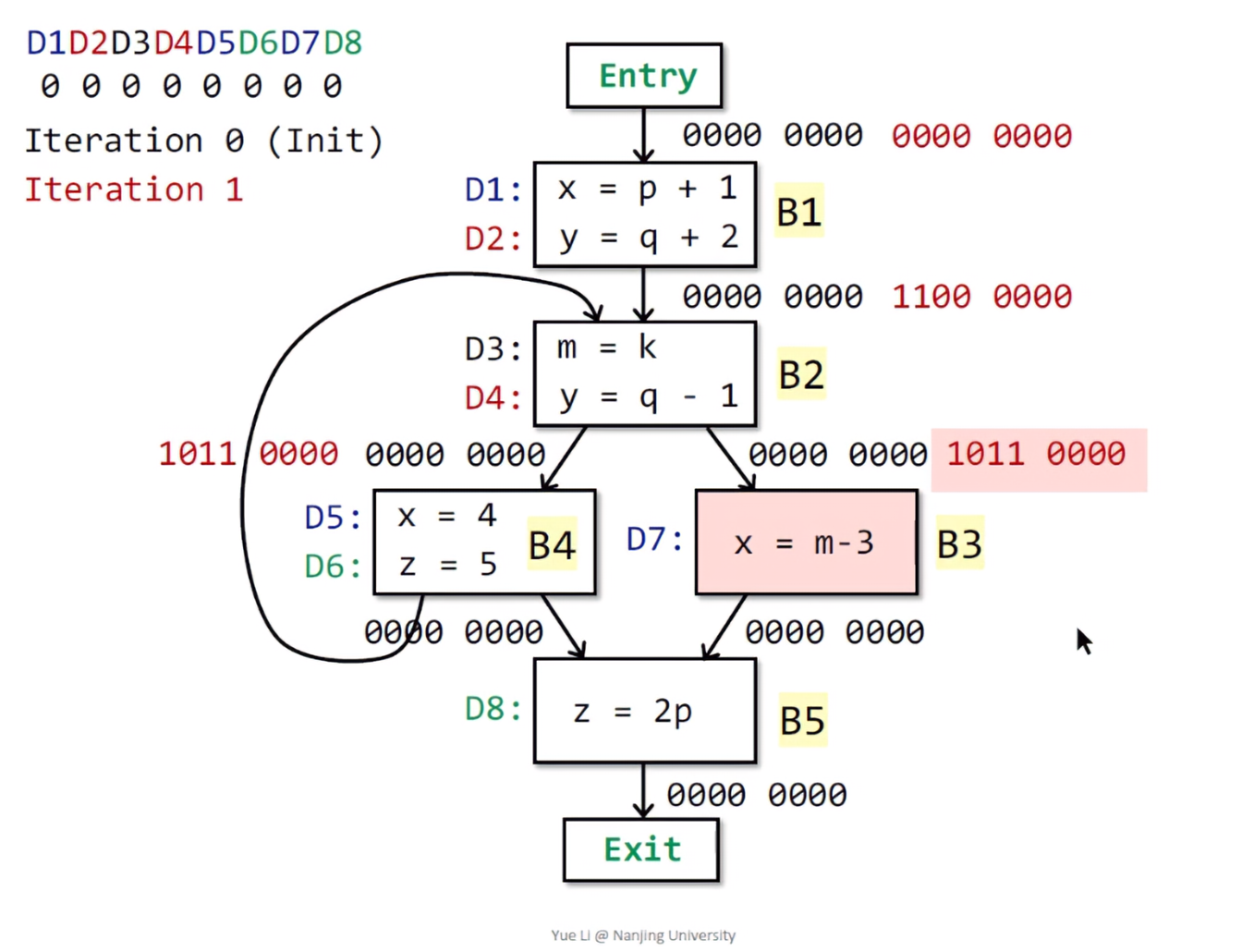
同样的，B3的前驱节点只有B2。其并集也就是B2[OUT] = 1011 0000 = B3[IN]。因为D7里的定义x，在D1存在重复定义，故将D1的位向量置0。根据公式，因为现在运行的D7存在重复定义的x，表示可以被到达，所以D7位会置1。故OUT[B3] = 0011 0010 。

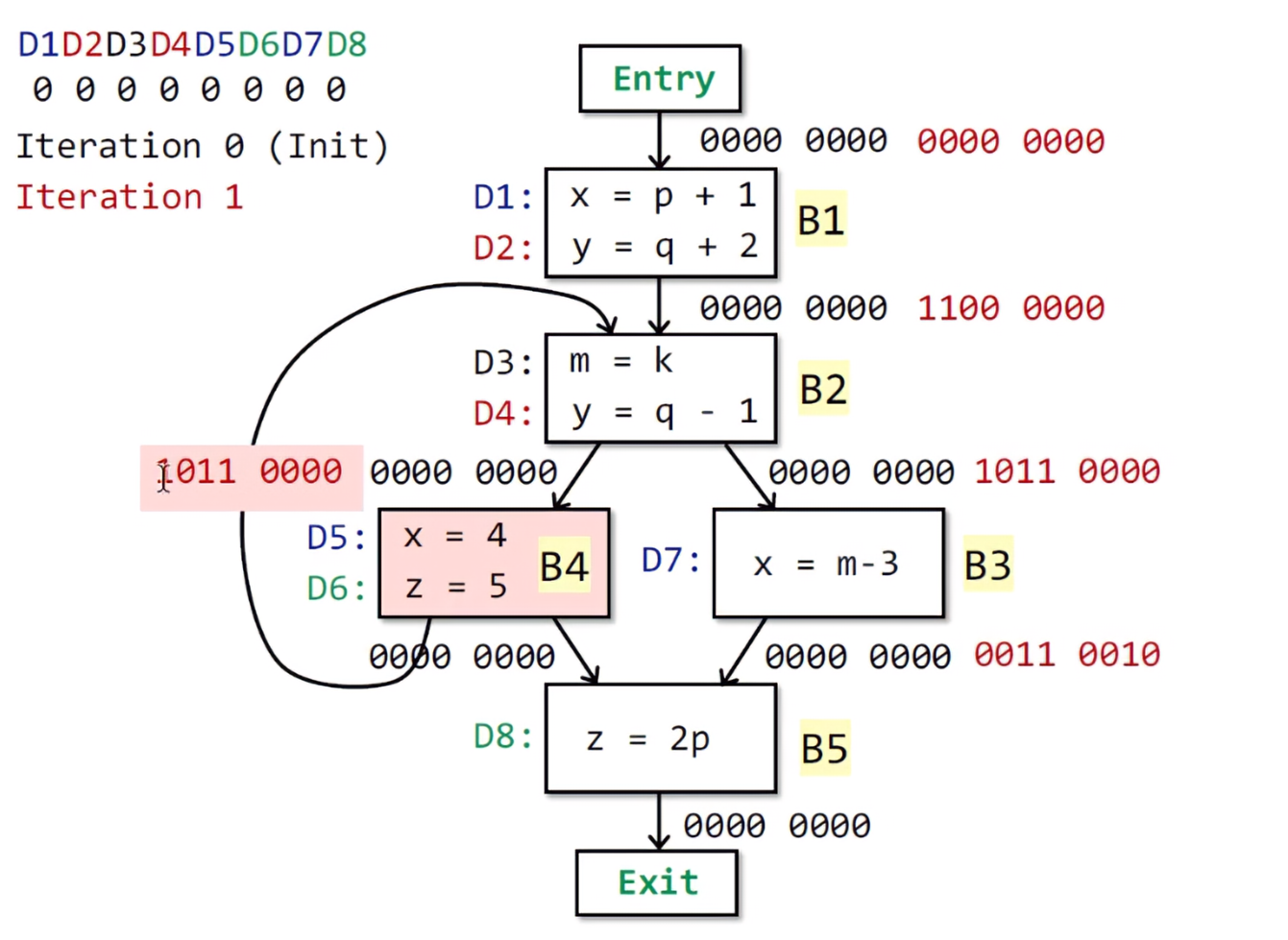
接下来顺序执行到B4，根据公式得到IN[B4] = 1011 0000，OUT[B4] = 0011 1100

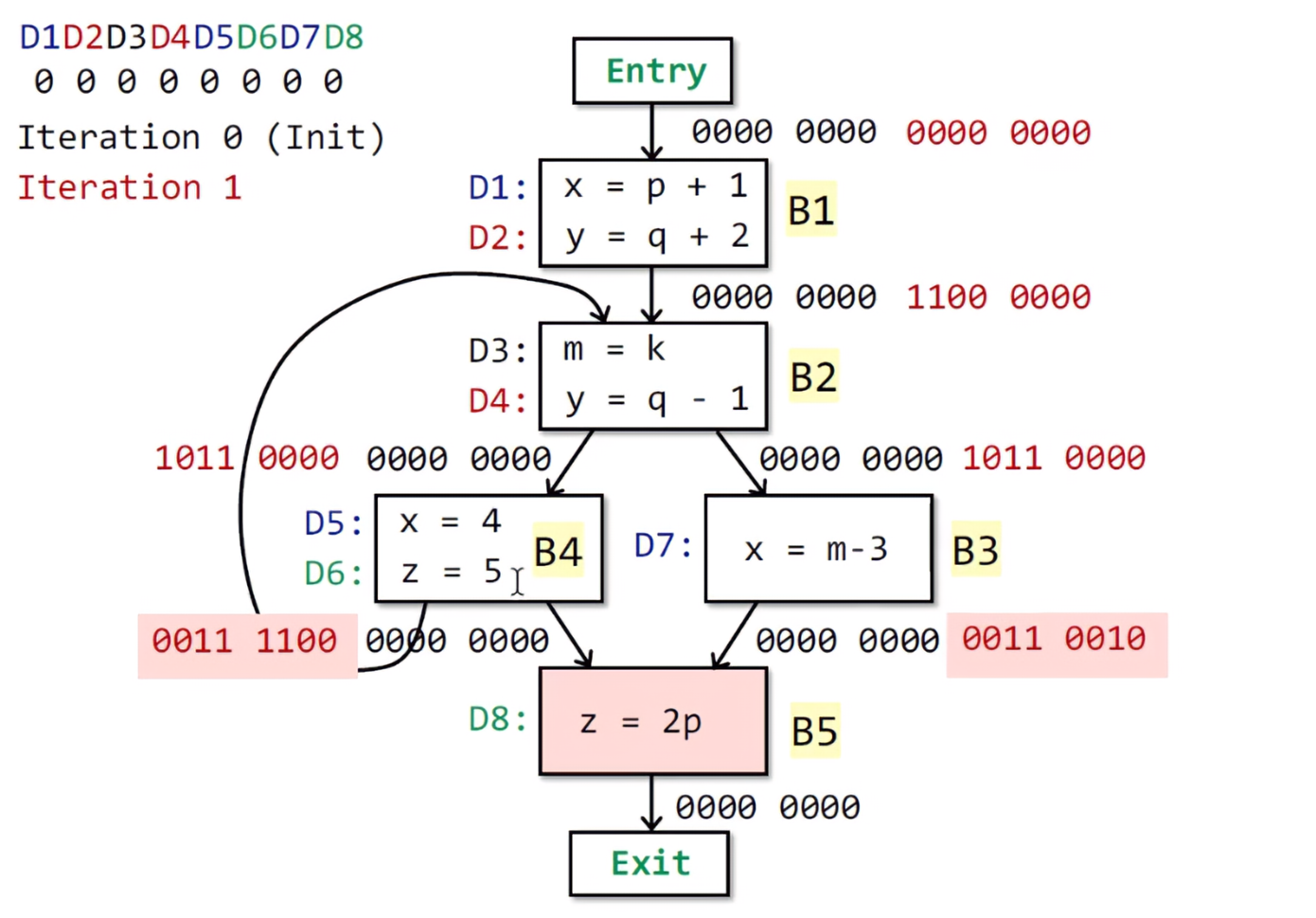
最后执行B5，根据公式计算：IN[B5] = 0011 1110，OUT[B5] = 0011 1011

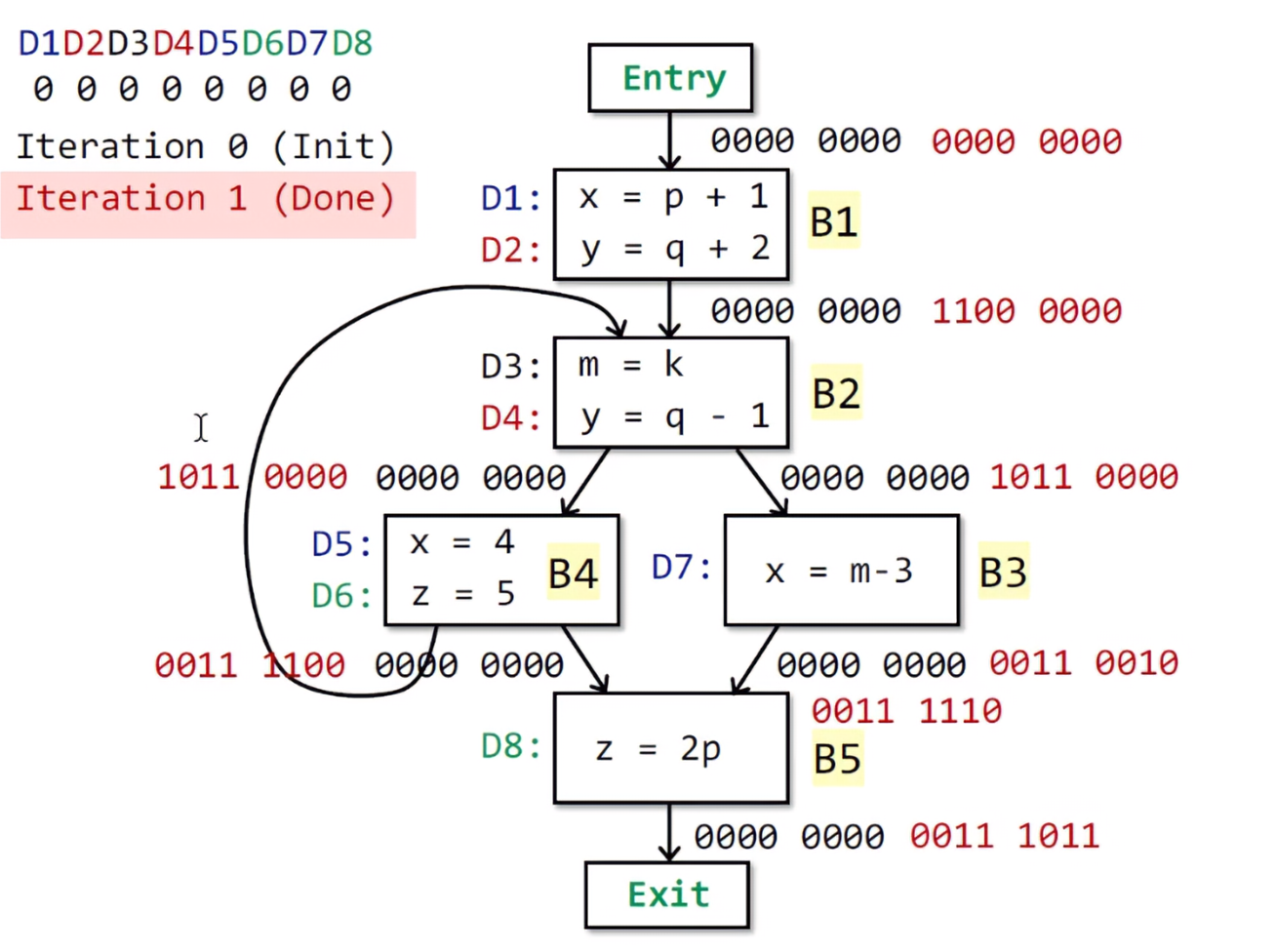
此时第一次遍历结束了，要不要进行第二次遍历，取决于每个BB的输出状态是否改变。在这里所有BB的状态都发生了改变，所以要进行第二次迭代。

B1[IN] = 0000 0000
B1[OUT] = 1100 0000

B2[IN] = B1[OUT_1] 1100 0000 ∪ B4[OUT_1] 0011 1100 = 1111 1100
B2[OUT] = 1011 1100

B3[IN] = 1011 1100
B3[OUT] = 0011 0110

B4[IN] = 1011 1100
B4[OUT] = 0011 1100

B5[IN] = B4[OUT] 0011 1100 ∪ B3[OUT] 0011 0110 = 0011 1110
B5[OUT] = 0011 1010

第二次迭代结束，因为发生了状态（B2、B3）的改变，依然需要第三次遍历。

B1[IN] = 0000 0000
B1[OUT] = 1100 0000

B2[IN] = B1[OUT_2] 1100 0000 ∪ B4[OUT_2] 0011 1100 = 1111 1100
B2[OUT] = 1011 1100

//此时输入和第二次遍历是一样的，所以此时输出也是一样的
B3[IN] = 1011 1100
B3[OUT] = 0011 0110

B4[IN] = 1011 1100
B4[OUT] = 0011 1100

B5[IN] = B4[OUT] 0011 1100 ∪ B3[OUT] 0011 0110 = 0011 1110
B5[OUT] = 0011 1010

此时已经不需要第四次遍历了，因为没有发生输出状态的改变。

通过这个例子可以发现，这个迭代最终是会停止的：

因为gen_s和kill_s在每次的迭代中都是保持不变的，在每次迭代的时候，会有一些新的facts加入到IN[S]，这些facts要么被kill掉，要么存活。一旦新的facts被加入到OUT[S]中，不管是加入到gen_s还是存活下来，它都会一直存在。并且OUT[S]不会发生从1->0的改变（只有0->1，或者1->1）。OUT[s]不会缩小，它只会变大。

一些个人的想法（不一定对）：这个算法的输出状态是以代码基本块的语句为单位的，每当块内语句出现一次新的定义变量，那么在位向量中，相应的位置就会置1；如果存在之前重复的定义变量，则将之前重复定义的语句对应的向量位置0，新定义的语句对应的向量位置1，表示该变量只有新语句有效。最后迭代完成后，每个代码块所达到的状态，就是位向量对应语句，在运行到该代码块时的有效状态。

以B2[OUT]为例，此时B2[OUT]代表的就是运行完B2之后，整个程序代码语句的有效状态。因为B2[OUT]为1011 1100，所以对于刚运行完B2这个时刻而言，语句D1、D3、D4、D5、D6都是有效代码：D1是对x的定义，截至到B2运行结束都是有效的；D3和D4都是B2的代码，刚刚运行完，自然也是有效代码；B4中的D5、D6对于B2而言，如果B4处于B2的前驱，此时D5、D6的重定义会影响到B2，表示D5、D6的重定义可以到达。而B3也重定义了x，但它不属于B2的前驱，不会影响B2。

Live Variables Analysis

Overview of Live Variables Analysis

Live variables analysis tells whether the value of variable v at program point p could be used along some path in CFG starting at p. If so, v is live at p; otherwise, v is dead at p.

首先存在一条路径，从p到结束，而且我们想知道变量v是否在p处存活，且v不应该被在被使用之前重定义。

• Information of live variables can be used for register allocations. e.g., at some point all registers are full and we need to use one, then we should favor using a register with a dead value.
  • 假设某刻存在所有寄存器都被写满（这一时刻也是program point），通过live variables分析我们可以知道哪个是dead value，从而替换掉dead value在寄存器里的值。如果使用掉其他正常的寄存器，可能会出现死机等情况。

Understanding Live Variables Analysis

• Data Flow Values/Facts

  • All the variables in a program

    • 在这个存活变量分析中，我们主要关注的就是程序中所有的变量

  • Can be represented by bit vectors

    • 这些facts可以用位向量表示

那么Live Variables Analysis应使用正向分析还是逆向分析，使得算法更加直观呢？实际上，在我们分析的过程中，没有必须用正向或逆向分析的说法；但是为了设计算法方便和直观，我们通常情况下使用backward analysis。

假如我们使用了Forward analysis，程序从顶向下分析，直到使用了变量v，才会给位向量置1. 但是，如果变量v到最后才会被使用，那么此时需要给已经分析过的代码状态全部置1（因为这里位向量表示的是所有变量全局的状态），就会和前面已经分析过的部分再次关联起来。而逆向分析从底向上，只要遇到哪个变量被使用就置1即可，此后在分析的过程中，就默认将位向量对应位置1了。

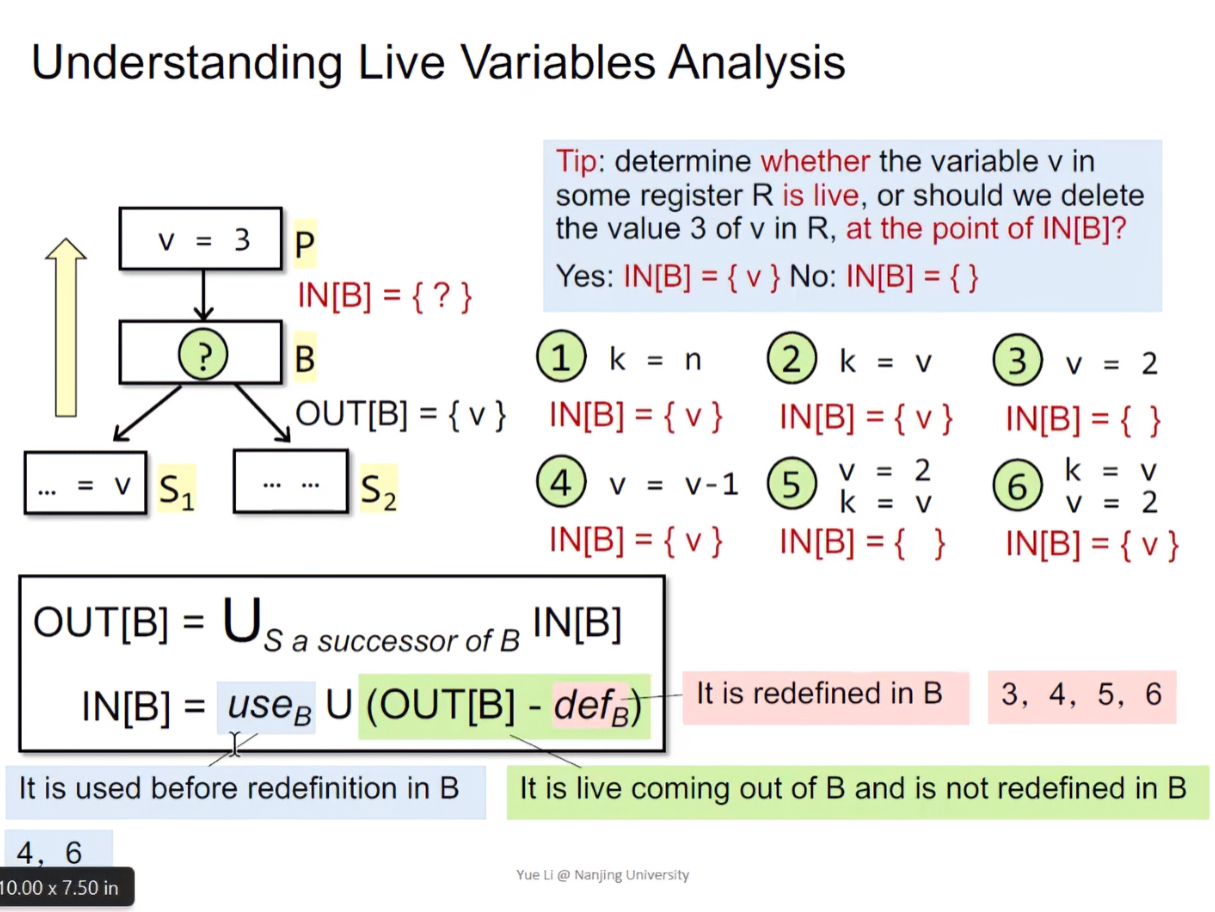
上图给出了一个简单的逆向分析例子。通过这个例子，我们可以列出公式，得到某个BB的存活变量状态。

勘误：上图中OUT[B]公式，等号右边IN[B]应该为IN[S]

首先是OUT[B]：

$$OUT[B] = ∪_{S\ a \ successor \ of \ B} \ IN[S]$$

这里B的输出等于所有B的后继节点输入的并集。因为只要B之后有任意一条路径，存在某一个变量v被使用，那么v在B的输出状态中依然时被使用的。

如果B中存在不同的代码语句，得到IN[B]的结果也不相同：

1. k = n
   1. 因为是从底向上分析，OUT[B]已知为v，而此时v没有被重定义（如果发生重定义，那么v就是一个dead code），且k没有用到，故存活变量状态就只有v
2. k = v
   1. 同上分析，v只是被使用，没有被重定义，所以还是v
3. v = 2
   1. 此时发生了重定义，所以v应该被删除
4. v = v - 1
   1. 这里是先将v使用（v - 1），然后在定义（v = v - 1），虽然v被重定义了，但是在重定义之前被使用了。在v-1这一刻，还是P里v=3的值，变量还是存活的
5. v = 2; k = v
   1. 这里讨论的是运行到B时，B之前的（也就是B的上半部分）变量存活情况，第一个语句是v = 2，表示变量v被重定义，也就是没用到p中定义的变量v，所以应该被舍弃。即使下条语句k = v用到了v，也不能置1。因为这个状态是表示该基本代码块之前的变量存活状态。
   2. 即使P里没有定义v，依然也需要将v的状态舍弃。我个人的理解是，因为在实际从底向上分析的时候，我们并不清楚程序上面的路径是否存在变量v的定义，所以这里依然需要置0。同样的，我觉得这种做法是为了符合sound和safe-approximation的原则。
6. k = v; v = 2；
   1. 与第四个情况相同，因为在运行到B的时候，v先被使用了，才被重定义，此时B中v的状态还是存活的
   2. 根据第四和第六的情况，我们可以简单理解成， 只要先赋值（使用）再定义，依然视为变量存活

根据上面的场景，我们可以得到IN[B]的公式：

$$IN[B] = use_B ∪ (OUT[B] - def_B)$$

这里的def_B自然指代的是B中重定义的变量（场景3、4、5、6），而重定义的变量需要从已使用的变量中剔除（也就是OUT[B]），最后和基本块中使用的变量取并集，就可以得到B最后的存活变量状态。

Algorithm of Live Variables Analysis（存活变量算法）

因为存活变量检测，是用backward analysis来实现，是给定OUT状态求解IN状态，故初始化的时候，应该对IN状态进行初始化。

注：一般情况下，may analysis的初始化是空集，而must analysis的初始化是ALL.

这个算法和之前的Reaching Definitions是很相似的，只是初始值和BB状态改变时的算法不同，其余运作原理都是一样的，这里不作赘述。

依旧来看一道和定义到达相似的例题：

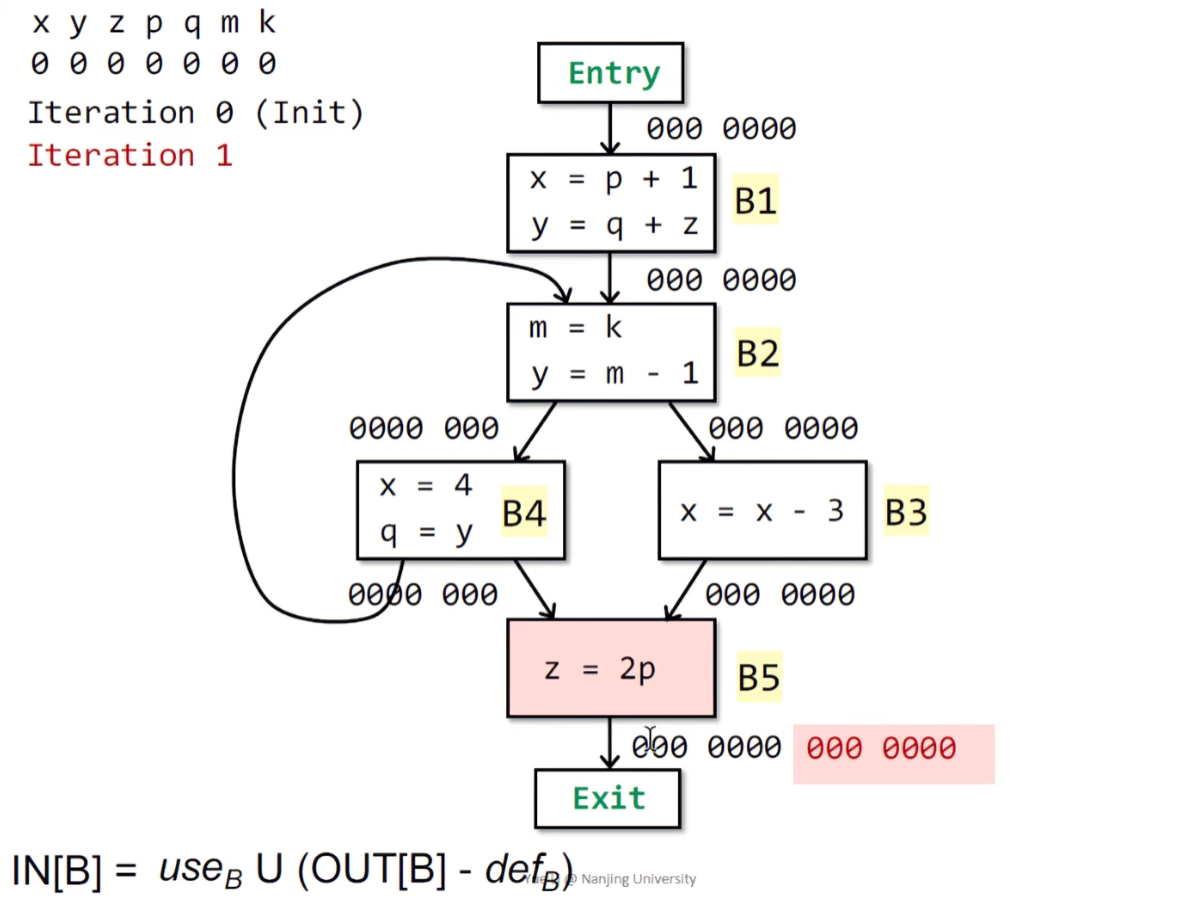
在这个例题中，我们将每一个变量的状态，组成一个位向量。根据算法，对所有BB的存活变量状态进行初始化，这里都是000 0000。按照自底向上的顺序，首先开始B5的运算。

由于B5没有后继节点，所以其输出态OUT[B5]=000 0000。在B5中，存在一个使用的变量p，故p位置1。所以B5的输入态IN[B5]=000 1000。

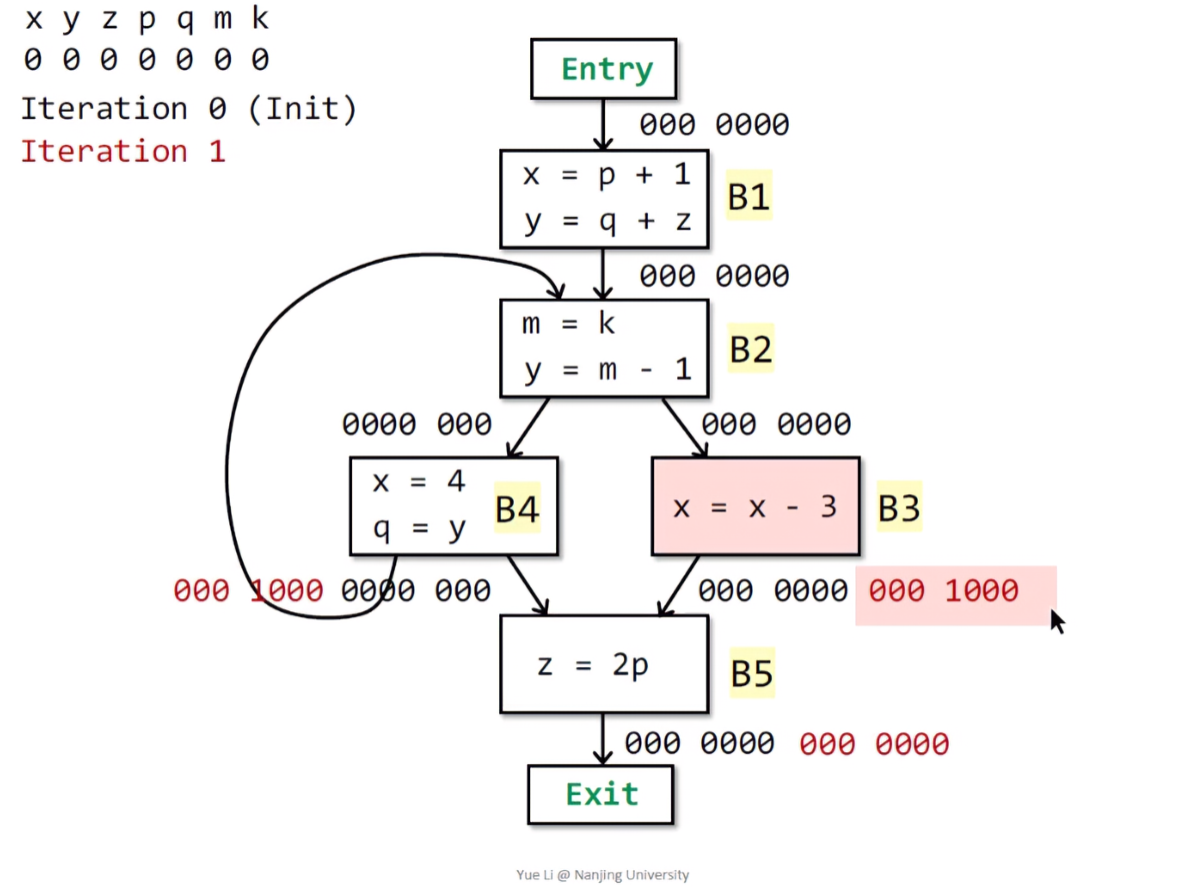
继续求B3，已知B3的输出态等于B5的输入态，故OUT[B3] = IN[B5] = 000 1000。跟据之前的情景实例，B3此处使用了x变量，之后再进行的重定义，所以x位依然置1，此时B3的输入态为IN[B3] = 100 1000。

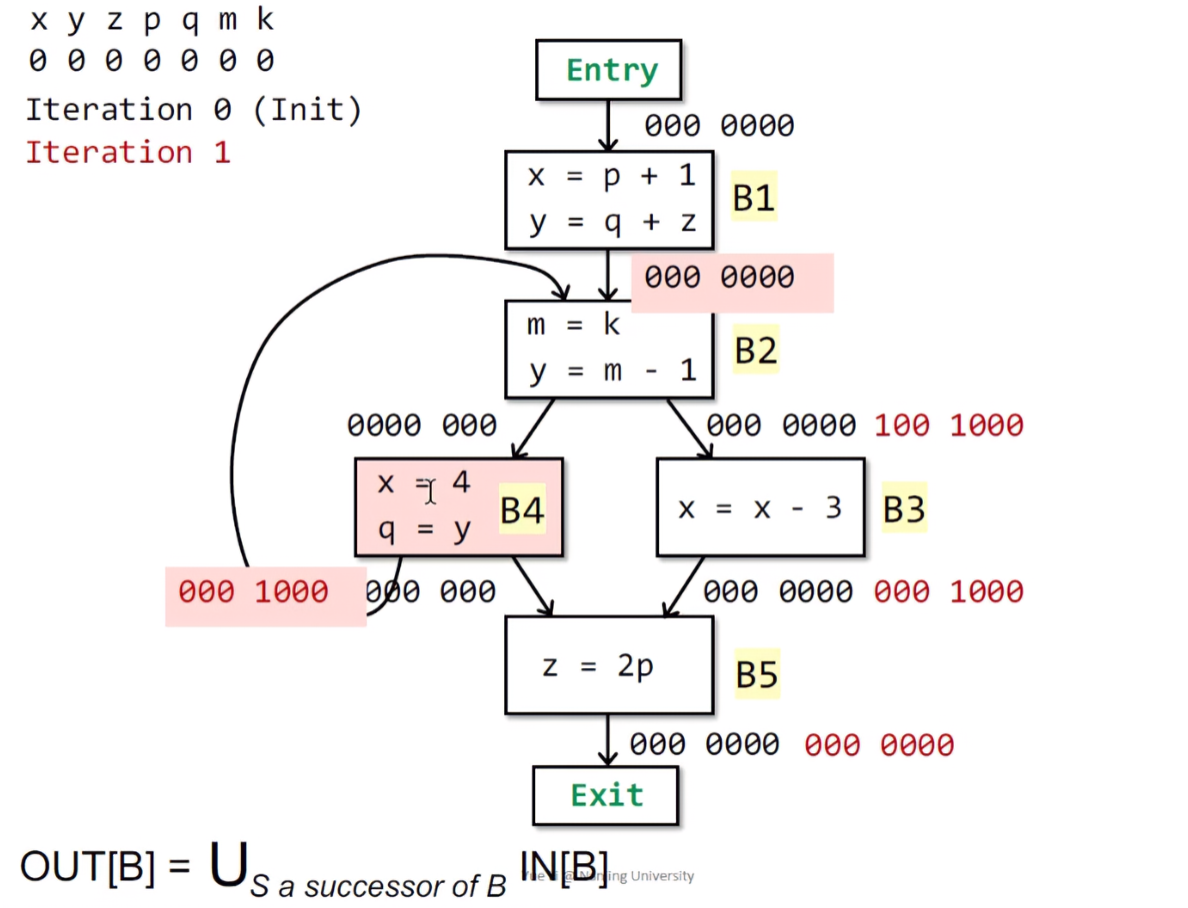
同理，B4的输出态就是其后继节点的输入态。这里B4存在两个后继节点：B5和B2。因为B2的初始输入态就是000 0000，之后并上B5的输入态仍然是IN[B5]本身，故OUT[B4] = IN[B5] = OUT[B3] = 000 1000。在B4中，首先对x进行了重定义，之后使用了y，定义了q。所以此处需要将y对应的标记为置1，得到IN[B4] = 010 1000。

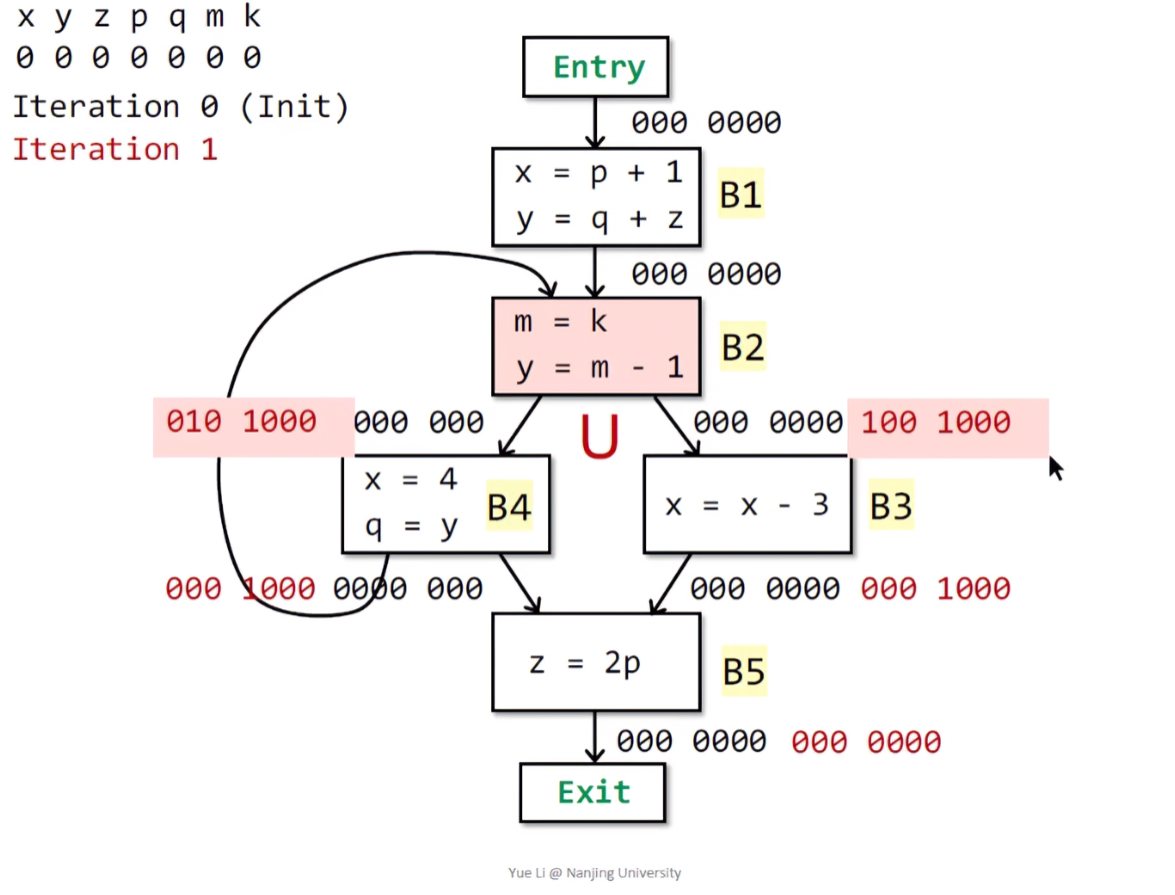
下一步来到B2，首先将B2的后继节点B4和B3进行union：IN[B4] ∪ IN[B3] = 010 1000 | 100 1000 = 110 1000 = OUT[B2]。分析B2中，变量k被使用，变量m先被重定义，之后又进行赋值使用，变量y被重定义，故k位置1、m位置0。因为y被重定义，所以这里应该删去y变量，最后的输出态应该为：IN[B2] = 100 1001。

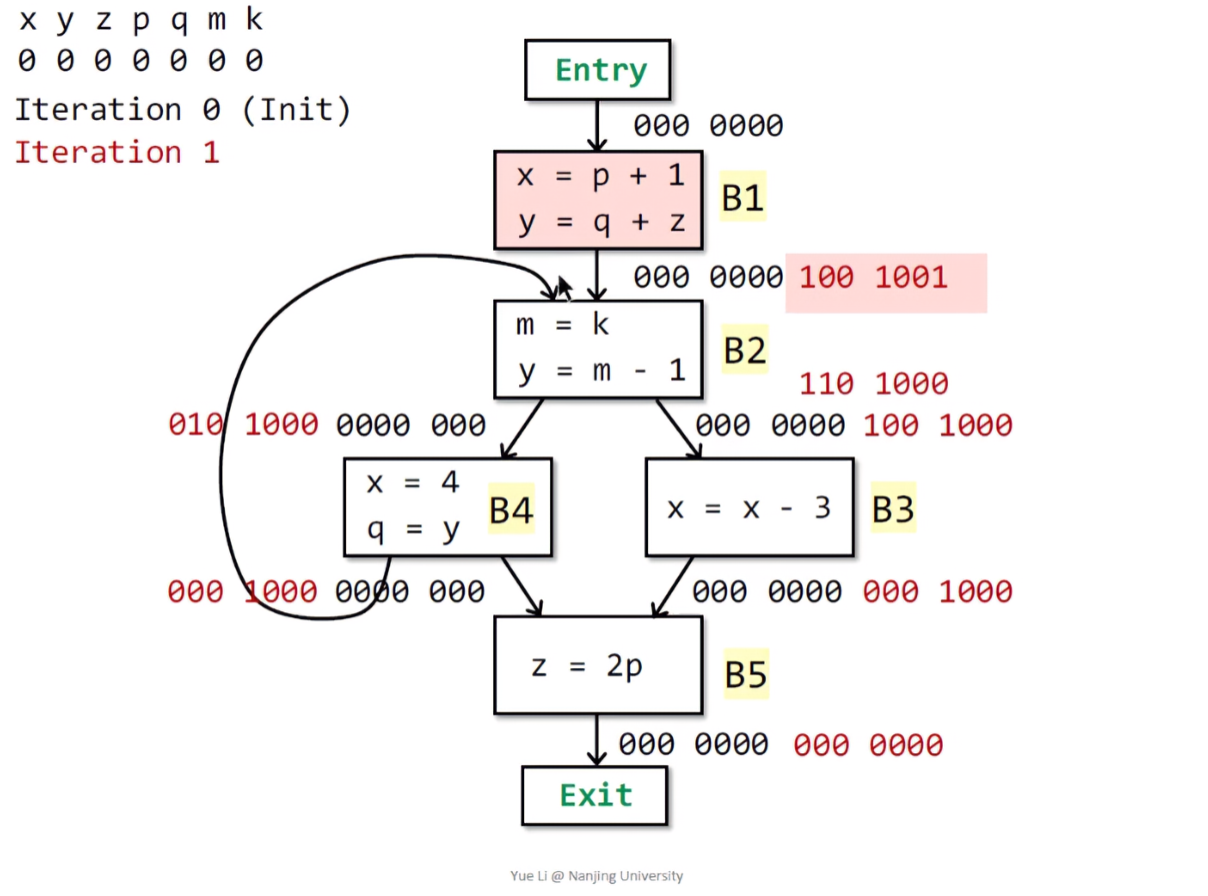
最后计算B1，根据公式，B1的输出太等于其后继节点B2的输入态：OUT[B1] = IN[B2] = 100 1001，且在B1种，变量p、q和z均被使用，而x和y也均发生重定义，所以p和q位置1，x和y位置0，得到B1的输入态IN[B1] = 001 1101。第一次遍历结束。

与定义到达算法相同，存活变量检测也需要进行迭代，直到所有的输入态满足约束条件，迭代才会停止。这里所有的基本快的输入态都变化了，所以需要有第二次遍历。同样的，定义到达是输入决定输出，一旦输入稳定，输出就不会变；这里也是如此，只要输出态不变，输入态就不会改变：

B5[OUT] = 000 0000
B5[IN] = 000 1000

B4[OUT] = B5[IN] | B2[IN_1] = 000 1000 | 100 1001 = 100 1001
B4[IN] = 010 1001

B3[OUT] = B5[IN] = 000 1000
B3[IN] = B3[IN_1] = 100 1000

B2[OUT] = B4[IN] | B3[IN] = 010 1001 | 100 1000 = 110 1001
B2[IN] = 100 1001

B1[OUT] = B2[IN] = 100 1001
B1[IN] = B1[IN_1] = 001 1001

此时B4的输入态发生改变，进行第三次迭代：

B5[OUT] = 000 0000
B5[IN] = 000 1000

//此时发现全部都没有变了
B4[OUT] = B5[IN] | B2[IN_2] = 000 1000 | 100 1001 = 100 1001
B4[IN] = 010 1001

B3[OUT] = B5[IN] = 000 1000
B3[IN] = B3[IN_1] = 100 1000

B2[OUT] = B4[IN] | B3[IN] = 010 1001 | 100 1000 = 110 1001
B2[IN] = 100 1001

B1[OUT] = B2[IN] = 100 1001
B1[IN] = B1[IN_1] = 001 1001

发现所有的BB状态稳定了，迭代完成。

Available Expressions Analysis

Overview of Available Expressions Analysis

An expression x op y is available at program point p if (1) all paths from the entry to p must pass through the evaluation of x op y, and (2) after the last evaluation of x op y, there is no redefinition of x or y.

如果或一个表达式在P点时可用的，那么也就意味着从入口到P点的所有路径，都必须执行x op y，并且在执行完这个语句后，没有发生x和y的重定义。

• The definition means at program p, we can replace expression x op y by the result of its last evaluation
• The information of available expressions can be used for detecting global common subexpressions.

Understanding Available Expressions Analysis

Available Expressions Analysis的数据流如下图所示，显然是一个正向分析。在执行语句之前，输入态存在a + b。而语句本身是a = x op y，那么我们需要将这个表达式以gen的形式加入到OUT里；并且要删除掉有关于a的定义：

在下面的示例中，a表达式走左侧路径，执行x重定义，根据规则，删除掉与x有关的表达式，在此时变为空集，并接着执行b表达式，仍然是e^16 * x和刚开始的a = e^16 * x是相同的，所以此时又把e^16 * x加入到集合中；在右侧路径，就直接到了最后，集合里的表达式没变，两者取交集（因为是所有路径都要满足，所以也是must analysis），得到这个表达式是存活的（也就是available）。

根据上面的步骤，可以得到IN[B]：

$$IN[B] = ∩_{P\ a \ predecessor \ of \ B} \ OUT[P]$$

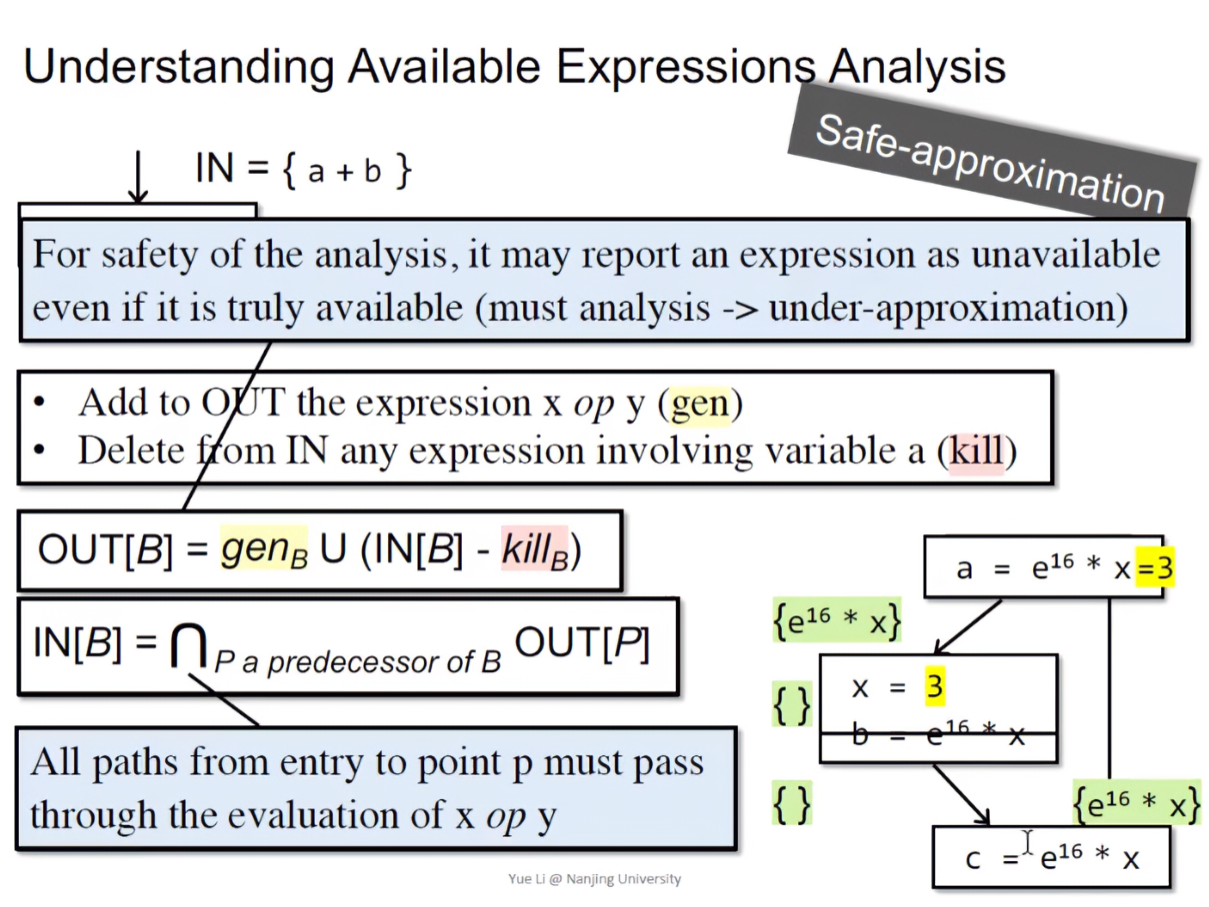
存活表达式分析也可能存在上图的情况，假设我们删去b表达式，当我们在进行存活表达式分析的时候，左侧路径分析x重定义，此时就应该删去，程序最后就是空集和表达式取交集，会得到这个表达式没有存活的结论。

但如果，左侧路径的x重定义为3，且表达式的x实际上也等于3，执行到程序最后表达式语义是没有问题的，这就会发生误报的现象。

Algorithm of Available Expressions Analysis（表达式存活算法）

在程序入口出去的时刻，可以看成程序没执行，自然就是空集。然后对每一个基本块初始化，因为这个分析是Must Analysis，所以初始化为all，就是位向量全置1. 假设初始化不是0，因为后面算法计算是涉及到交集，0和任何数的交集都是0，就没有意义了。

依旧看一道例题，首先对程序entry的出口初始化为0，其余基本块的输出状态全置1. 将程序中所有表达式提取出来，组成位向量如图所示：

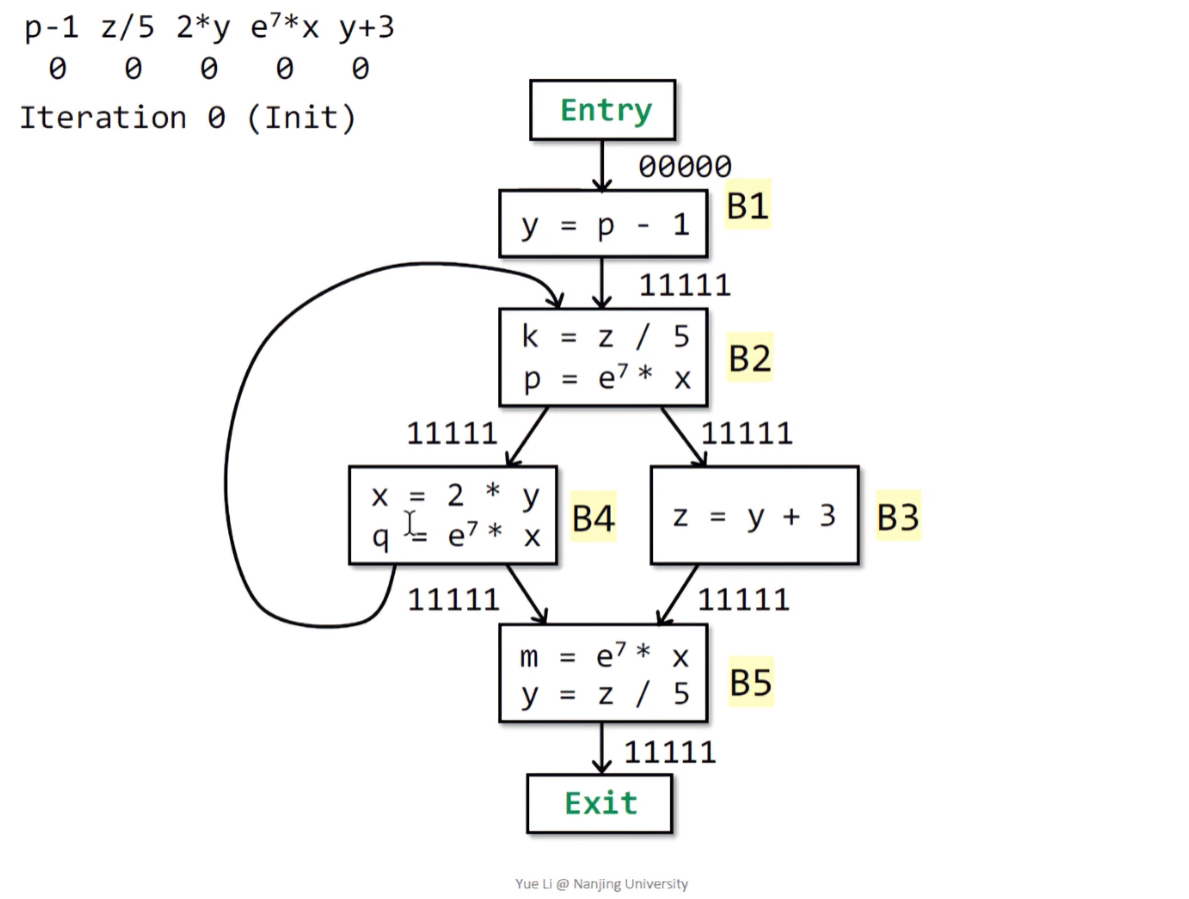
首先分析B1，按照算法，因为B1没有前驱节点，只需要将B1的表达式置1即可，就是OUT[B1] = 10000。

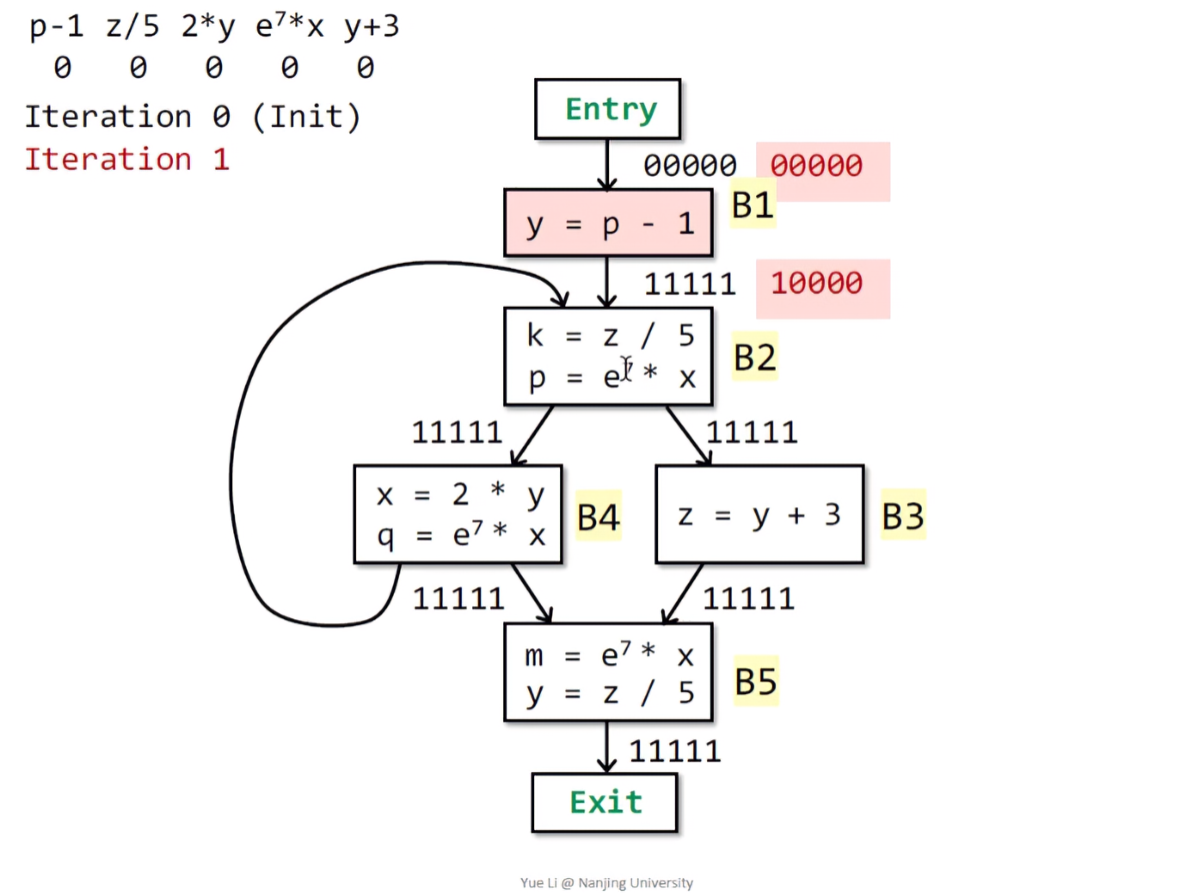
接着分析B2，首先B2的两个前驱节点B1和B4的输出态取交集IN[B2] = OUT[B1] ^ OUT[B4] = 10000，且B2有两个表达式，但e^7 * x和前驱节点B4冲突，所以从IN[B2]中删除掉冲突的表达式（这里已经为0）；此外，这里p发生了重定义，所以应该删除p-1。然后对应向量位置1：OUT[B2] = 01010 | 00000 = 01010。

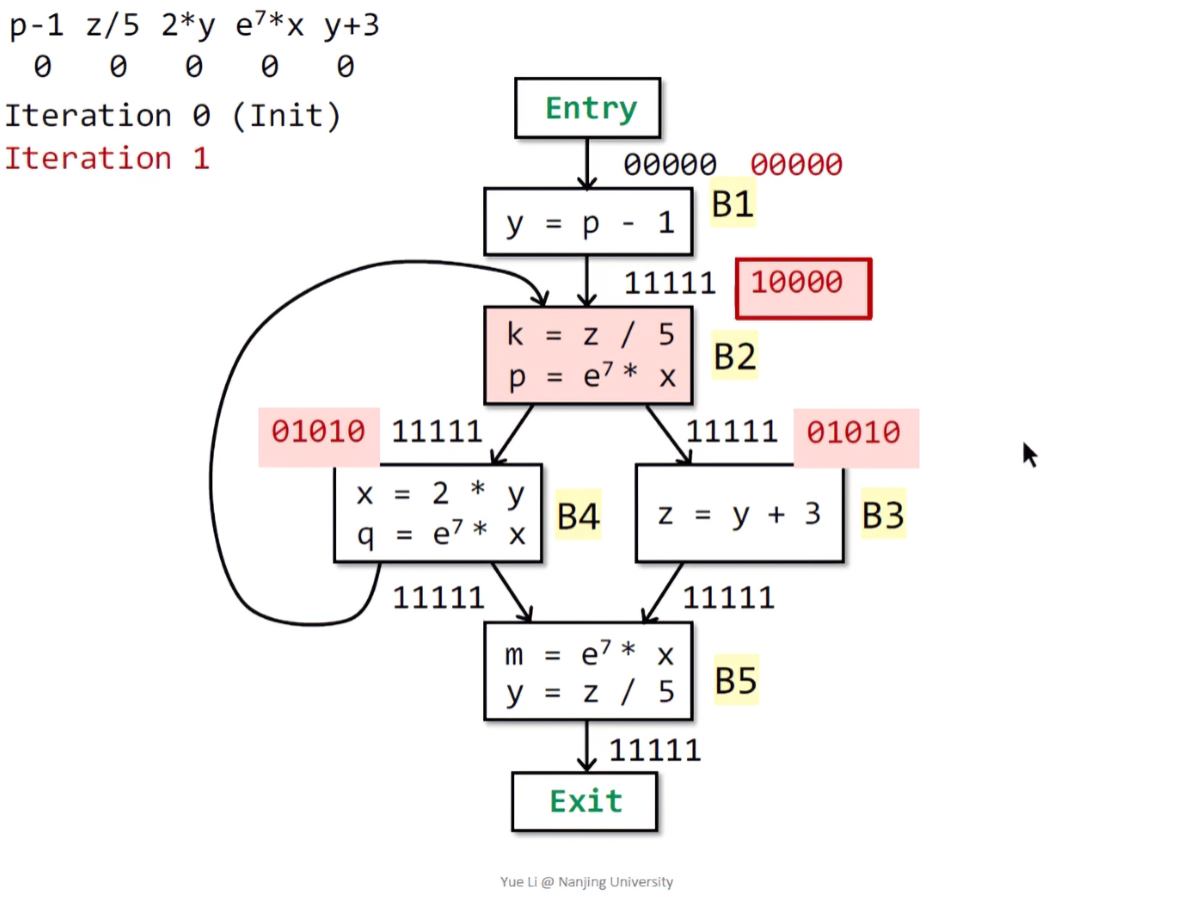
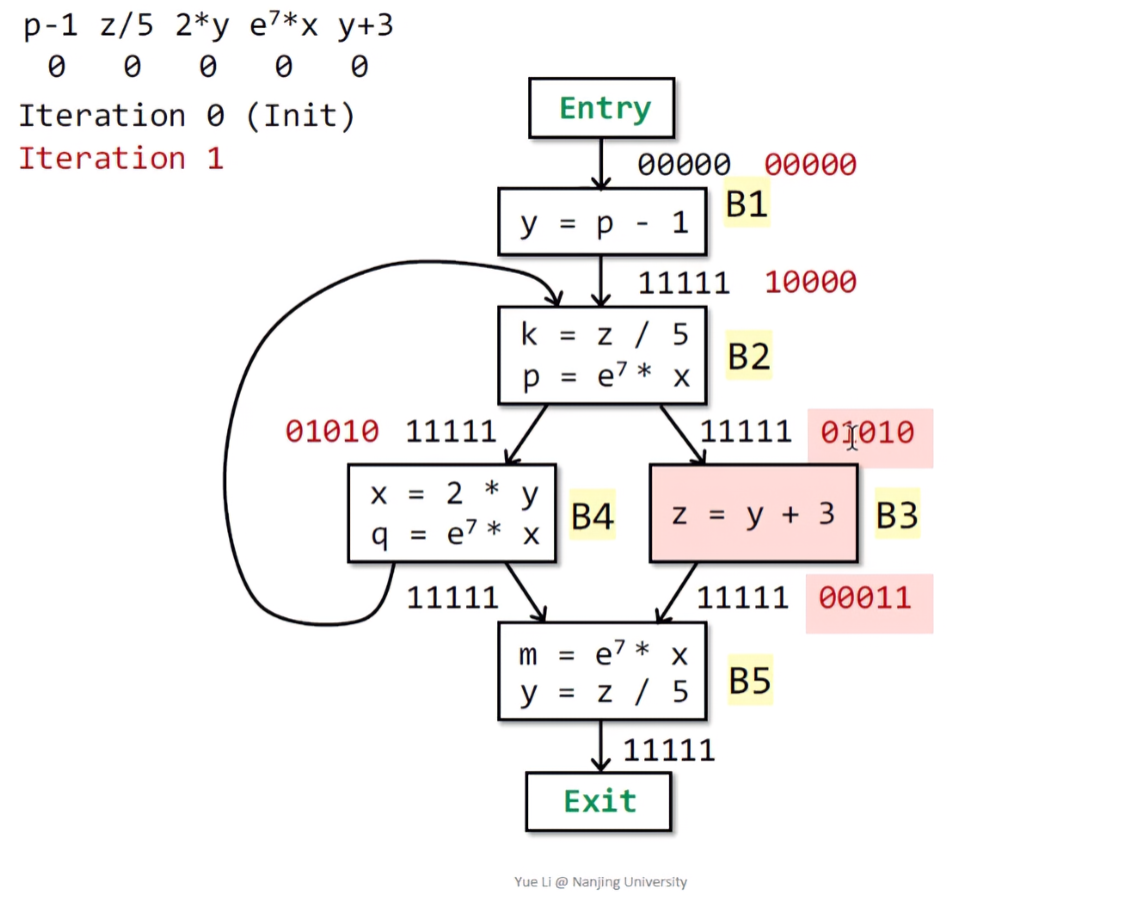
下面进入B3，由公式得IN[B3] = OUT[B2] = 01010 ，且在B3中存在z的重定义，所以删去z / 5，得到IN[B3] = 00001 | 00010 = 00011 ：

继续到B4，B4的输入IN[B4] = OUT[B2] = 01010，输出OUT[B4] = 00110 | 01010 = 01110:

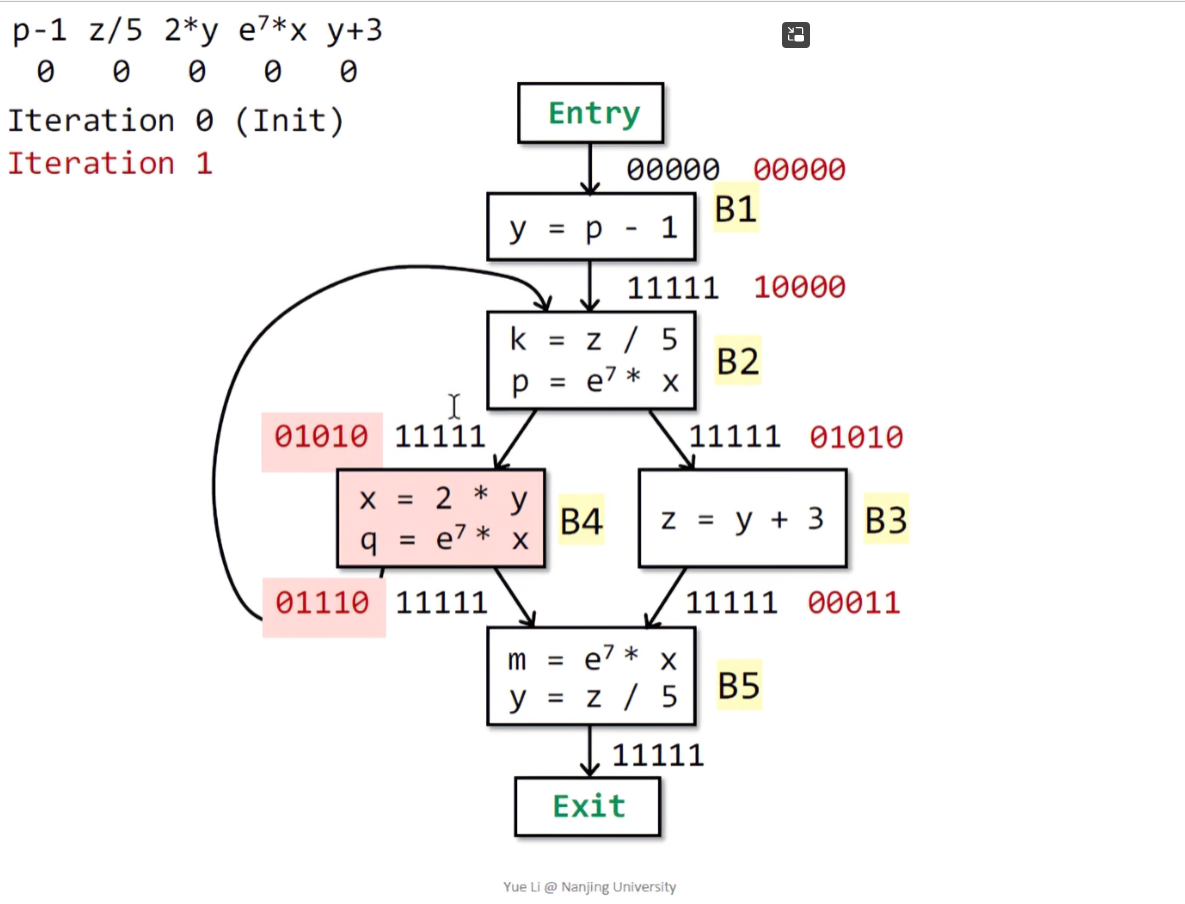
最后运行到B5，得到IN[B5] = OUT[B4] ^ OUT[B3] = 01110 ^ 00011 = 00010，在B5中存在两个表达式，而y表达式发生了重定义，故删去2 * y和y + 3，最后得到OUT[B3] = 01010 | 00010 = 01010 :

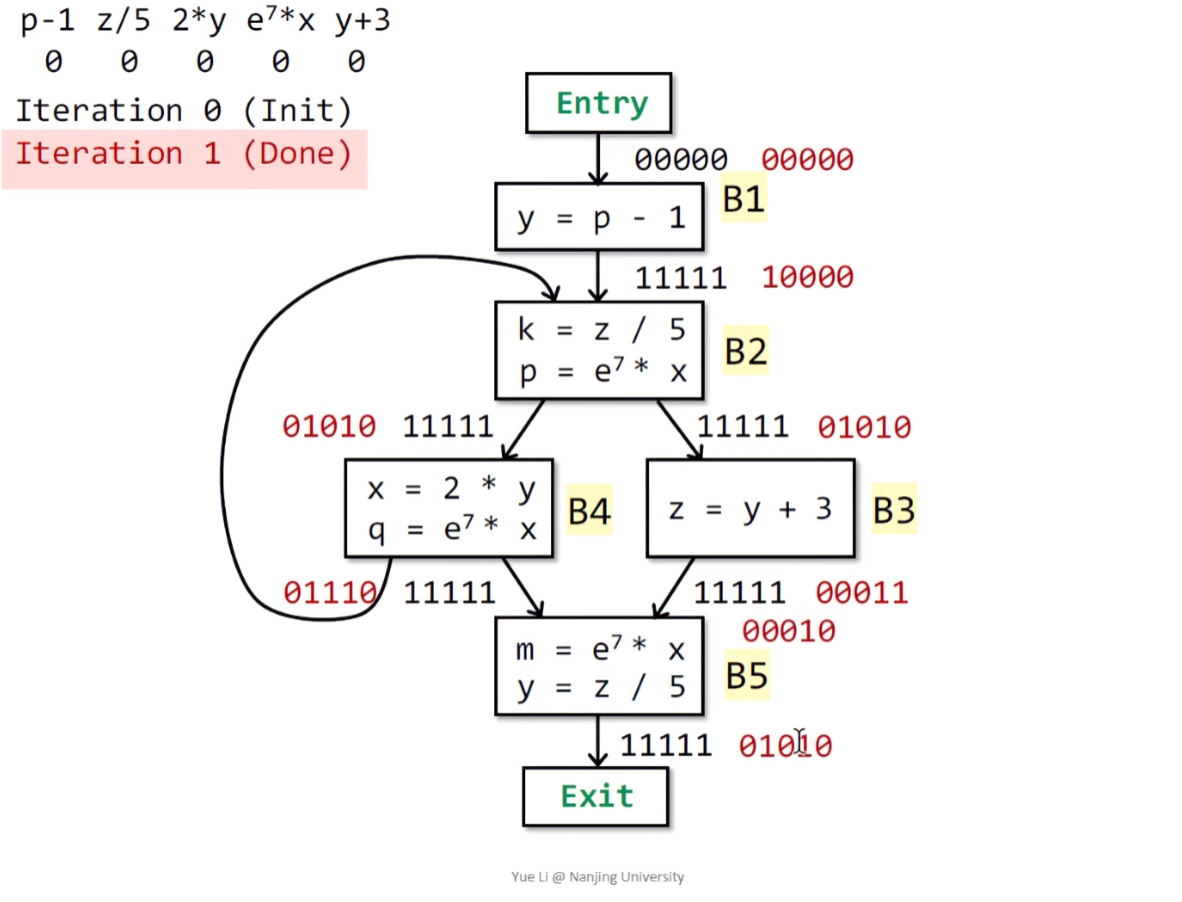
第一次迭代结束，因为所有的输出状态值都变化了，所以继续第二次遍历：

B1[IN] = 00000
B1[OUT] = 10000

B2[IN] = B1[OUT] ^ B4[OUT_1] = 10000 ^ 01110 = 00000
B2[OUT] = 01010

B3[IN] = B2[OUT] = 01010
B3[OUT] = 00011

B4[IN] = B2[OUT] = 01010
B4[OUT] = 01110

B5[IN] = 00010
B5[OUT] = 01010

因为输出状态值和第一次一样，所以就不需要第三次遍历了。

Analysis Comparision

	Reaching Definitions	Live Variables	Available Expressions
Domain(集合)	定义	变量	表达式
Direction	正向	反向	正向
May/Must	May	May	Must
Boundary(边界)	OUT[entry]=∅	IN[exit]=∅	OUT[entry]=
Initialization	OUT[B]=∅	IN[B]=∅	OUT[∅]=∪
Transfer function	见算法	见算法	见算法
Meet(merge处理)	∪	∪	∩

Foundations

Iterative Algorithm for May & Forward Analysis

View Iterative Algorithm in Another Way

• Given a CFG(Program) with k nodes, the iterative algorithm updates OUT[n] for every node n in each iteration.
  • 假设一个控制流图有k个节点，在每次遍历的时候，我们用OUT[n]表示该点在该次遍历中更新的信息
• Assume the domain of the values in data flow analysis is V, then we can define a k-tuple: (OUT[n1], OUT[n2], OUT[n3], ..., OUT[nk])as an element of set(V₁ × V₂ × … × V_k) denoted as V^k, to hold the values of the analysis after each iteration.
  • 假设在控制流中值域为V，那么我可以定义一个k元组，每个node的状态值将会组成某一次迭代的V_n，而V_n作为所有V集合的一个元素。
• Each iteration can be considered as taking an action to map an element of V^k to a new element of V^k, through applying the transfer functions and control-flow handing, abstracted as a function: F: V^k -> V^k
  • 这样，每次迭代就可以看成V^k中的一个元素，通过转换函数或控制流处理，映射到V^k中的另一个元素。因为存在映射关系，所以就可以抽样成函数的形式。
• Then the algorithm outputs a series of k-tuples iteratively until a k-tuple is the same as the last one in two consecutive iterations.
  • 之后算法会迭代输出一系列的k元组，直到最后两个连续的k元组的完全相同，迭代才结束。

上图用数学语言表示了算法的过程。首先初始化过程，使用bottom符号表示置空，将程序初始化时的值域称为X₀；在第一次迭代的过程中，v的下标表示节点，上标表示迭代次数，同样将第一次迭代的值域称为X₁，也就等于F(X₀)。同样的，直到最后的值域不在发生改变，即X_i等于X_i+1，我们可以得到F(X_i)=X_i。

X is a fixed point of function F if F(x) = x. 即这个算法达到了不动点（算法可以停止）。

The iterative algorithm (or the IN/OUT equation system) produces a solution to a data flow analysis:

• Is the algorithm guaranteed to terminate or reach the fixed point, or does it always have a solution?
  • 这个算法一定能达到不动点吗？（一定能停止吗？）
    • 一定能达到不动点
• If so, is there only one solution or only one fixed point? If more than one, is our solution the best one(most precise)?
  • 假设能达到不动点，那不动点是只有一个吗？那我们求解出来的不动点是最佳答案吗？（是最精确的吗？）
• When will the algorithm reach the fixed point, or when can we get the solution?
  • 我们什么时候能够到达不动点？

Partial Order

We define poset（偏序集） as a pair(P, ≤) where ≤ is a binary relation that defines a partial ordering over P, and ≤ has the following properties:

1. 自反性（Reflextivity）：对于任意x∈P, x ≤ x
2. 反对称性（Antisymmetry）：对于任意x, y∈P, x ≤ y ^ y ≤ x -> x = y，x偏序y的同时y也偏序于x，则x和y相等
3. 传递性（Transitivity）：对于任意x, y, z∈P, x ≤ y ^ y ≤ z -> x ≤ z，x偏序于y，y偏序于y，则x偏序于z

示例，整数集和小于等于关系满足偏序集吗？**答案是满足，回答如上图。**如果改成整数集和小于，那满足偏序集吗？答案是不满足，因为是不满足自反性（1不会小于1）。

Upper and Lower Bounds（上界和下界）

给定一个偏序集（P，≤）和它一个子集S，并且S也是P的子集。那么，对于任意的x∈S，x都偏序（≤）u，我们就称u∈P是S的一个上界。相近的，如果l∈P是S的下界，那么对于集合S的任意元素x，都存在l偏序于x。

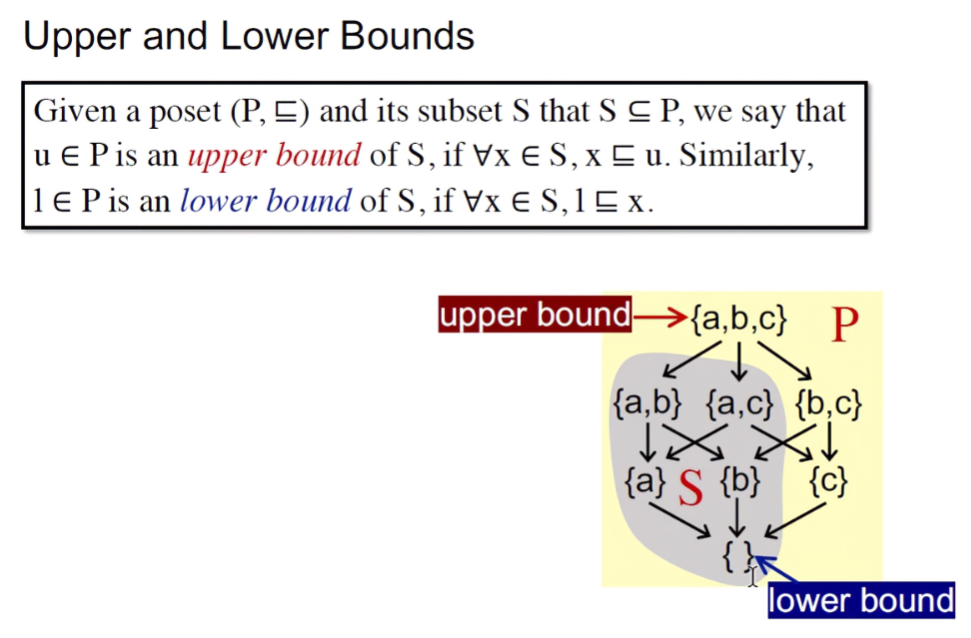
最小上界（least upper bound, lub or join）：对于S的任意一个上界u，都存在最小上界偏序于u。

最大下界（greatest lower bound, glb or meet）：对于S的任意一个下界l，都存在l偏序于最大下界。

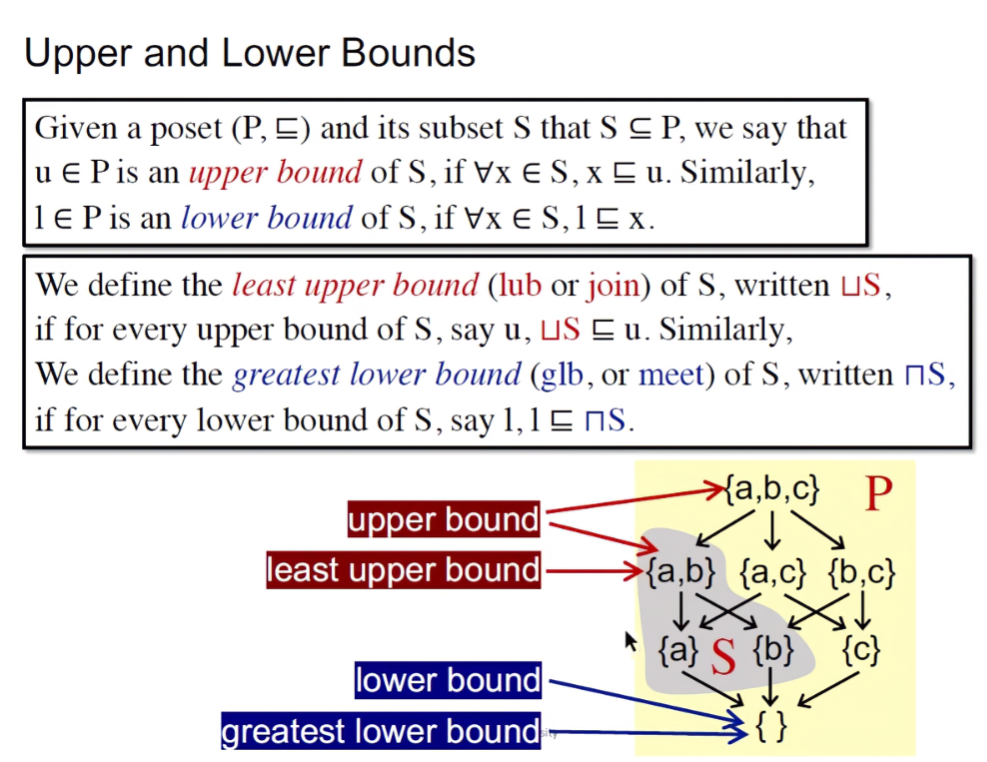
如果集合S里面只有两个元素a和b，那么S的上下界表示如下：

Some Properties

1. Not every poset has lub or glb，不是所有的偏序集都有最大下界和最小上界
2. But if a poset has lub or glb, it will be unique，如果一个偏序集有最大下界或最小上界，那么它有且仅有一个（反对称性可以证明）

Lattice(格) and Semilattice

给定一个偏序集，对于P中的任意a, b两个元素，如果a和b组成的最大下界和最小上界都存在，那么就叫这个偏序集叫做lattice。换句话说，对于lattice里的每一个元素，都有最小上界和最大下界。

同样的，给定一个偏序集，对于P中任意的元素a和b：如果a和b只能组成最大上界，那么将这个偏序集称为join semilattice; 反之，若只能组成最小下界，那么称为meet semilattice.

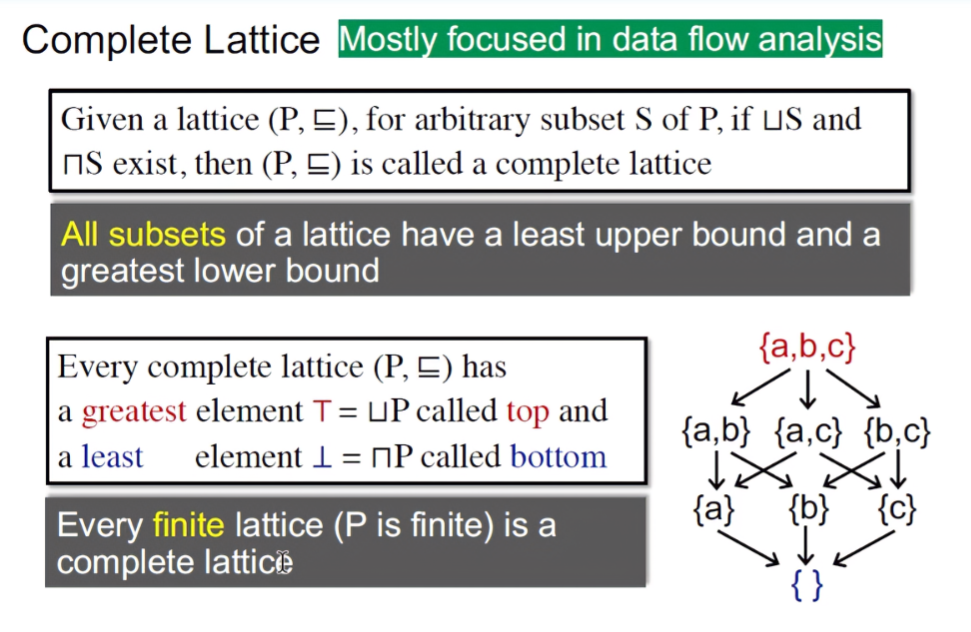
Complete Lattice

给定一个格（P，≤），对于P的任意子集S，若S的最小上界和最大下界均存在，那么这个格会被称为全格。也就是说，全格的所有子集，都至少有一个最大下界和最小下界。

Product Lattice

Data Flow Analysis Framework via Lattice

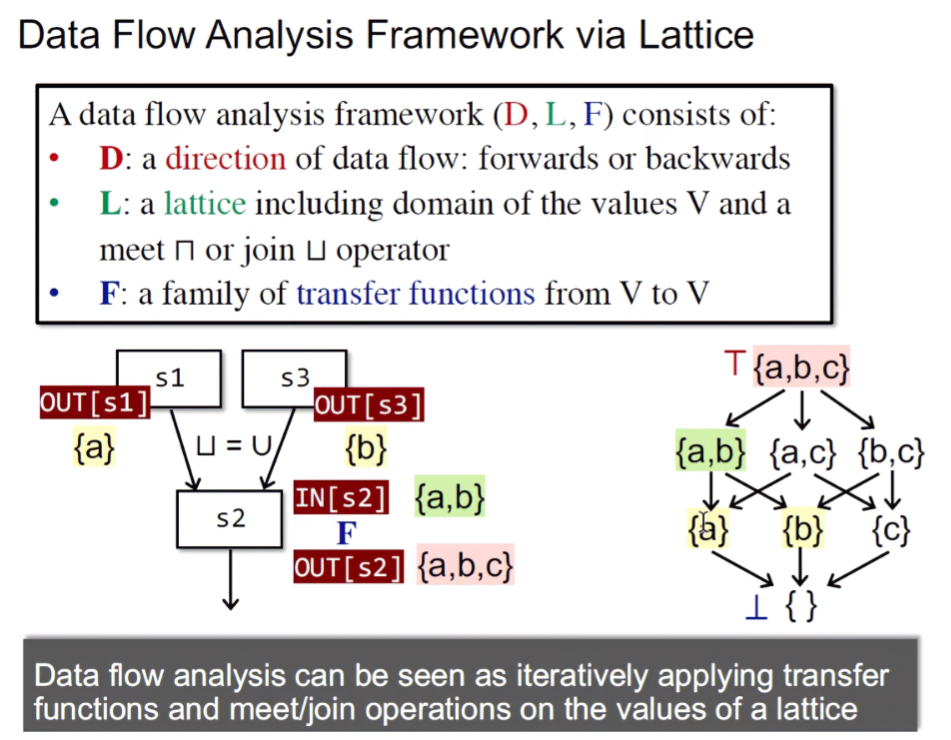
A data flow analysis framework(D, L, F) consists of:

• Direction: a direction of data flow: forwards or backwards
• Lattice: a lattice including domain of the values V and a meet or join operator
• Functions: a family of transfer functions from V to V

Monotonicity and Fixed-Point Theorem